Optimizing a Math Expression Parser in Rust

Optimizing a Math Expression Parser in Rust
- 44 minsOptimizing a Math Expression Parser in Rust
Table of contents
In a previous post I explored how to optimize file parsing for max speed. This time, we’ll look at a different, self-contained problem: writing a math expression parser in Rust, and making it as fast and memory-efficient as possible.
Let’s say we want to parse simple math expressions with addition, subtraction, and parentheses. For example:
4 + 5 + 2 - 1 => 10
(4 + 5) - (2 + 1) => 6
(1 + (2 + 3)) - 4 => 2
We’ll start with a straightforward implementation and optimize it step by step.
YOU CAN FIND THE FULL CODE ON: https://github.com/RPallas92/math_parser
Baseline implementation (43.1 s)
Here’s the first version of our parser:
use std::fs;
use std::io::Result;
use std::{iter::Peekable, time::Instant};
fn main() -> Result<()> {
let total_start = Instant::now();
let mut step_start = Instant::now();
let input = read_input_file()?;
println!("Step 1: Input file read in {:?}", step_start.elapsed());
step_start = Instant::now();
let result = eval(&input);
println!(
"Step 2: Calculation completed in {:?}",
step_start.elapsed()
);
let total_duration = total_start.elapsed();
println!("--- Summary ---");
println!("Result: {}", result);
println!("Total time: {:?}", total_duration);
Ok(())
}
fn read_input_file() -> Result<String> {
fs::read_to_string("data/input.txt")
}
fn eval(input: &str) -> u32 {
let mut tokens = tokenize(input).into_iter().peekable();
parse_expression(&mut tokens)
}
fn tokenize(input: &str) -> Vec<Token> {
input
.split_whitespace()
.map(|s| match s {
"+" => Token::Plus,
"-" => Token::Minus,
"(" => Token::OpeningParenthesis,
")" => Token::ClosingParenthesis,
n => Token::Operand(n.parse().unwrap()),
})
.collect()
}
fn parse_expression(tokens: &mut Peekable<impl Iterator<Item = Token>>) -> u32 {
let mut left = parse_primary(tokens);
while let Some(Token::Plus) | Some(Token::Minus) = tokens.peek() {
let operator: Option<Token> = tokens.next();
let right = parse_primary(tokens);
left = match operator {
Some(Token::Plus) => left + right,
Some(Token::Minus) => left - right,
other => panic!("Expected operator, got {:?}", other),
}
}
return left;
}
fn parse_primary(tokens: &mut Peekable<impl Iterator<Item = Token>>) -> u32 {
match tokens.peek() {
Some(Token::OpeningParenthesis) => {
tokens.next(); // consume '('
let val = parse_expression(tokens);
tokens.next(); // consume ')'
}
_ => parse_operand(tokens),
}
}
fn parse_operand(tokens: &mut Peekable<impl Iterator<Item = Token>>) -> u32 {
match tokens.next() {
Some(Token::Operand(n)) => n,
other => panic!("Expected number, got {:?}", other),
}
}
#[derive(Debug, Clone, PartialEq)]
enum Token {
Operand(u32),
Plus,
Minus,
OpeningParenthesis,
ClosingParenthesis,
}
How it works
Let’s break it down.
The program reads from a file called input.txt, which contains a math expression in a single line. That expression is passed to the eval() function.
The tokenize() function processes the input string, splitting it by whitespace and converting each segment into a token. For example, this input:
7 - 3 + 1
…is turned into this list of tokens:
[Operand(7), Minus, Operand(3), Plus, Operand(1)]
The parser then uses a simple recursive strategy:
parse_expression()handles sequences of additions and subtractions.parse_primary()handles numbers and expressions inside parentheses.parse_operand()handles the actual integer values.
The recursive call to parse_expression() inside parse_primary() allows us to evaluate nested expressions (parentheses).
Parser Example: (1 + 2) - 3
Let’s walk through parsing the expression (1 + 2) - 3 using our functions:
fn eval(input: &str) -> u32 {
let mut tokens = tokenize(input).peekable();
parse_expression(&mut tokens)
}
Input string: (1 + 2) - 3
Tokens with index:
| Index | Token |
|---|---|
| 0 | OpeningParenthesis ( |
| 1 | Operand(1) |
| 2 | Plus + |
| 3 | Operand(2) |
| 4 | ClosingParenthesis ) |
| 5 | Minus - |
| 6 | Operand(3) |
We begin by calling parse_expression at depth 1:
parse_expression(depth 1)- Calls
parse_primaryto get the first value.
- Calls
parse_primary(depth 2)- Sees
OpeningParenthesisat index 0. - Consumes
(and callsparse_expression(depth 3) for the parenthesized subexpression.
- Sees
parse_expression(depth 3)- Calls
parse_primary(depth 4).
- Calls
parse_primary(depth 4)- Sees
Operand(1)at index 1. - Calls
parse_operand(depth 5), which consumes index 1 and returns1.
- Sees
parse_expression(depth 3) (resuming)- Sees
Plusat index 2. - Consumes
+and callsparse_primary(depth 4) again.
- Sees
parse_primary(depth 4)- Sees
Operand(2)at index 3. - Calls
parse_operand(depth 5), which consumes index 3 and returns2.
- Sees
parse_expression(depth 3)- Combines
1 + 2 = 3. - Returns
3to the caller at depth 2.
- Combines
parse_primary(depth 2) (resuming)- Now at index 4 sees
ClosingParenthesis. - Consumes
)and returns the inner value3.
- Now at index 4 sees
parse_expression(depth 1) (resuming)- Left side is
3. - Sees
Minusat index 5. - Consumes
-and callsparse_primary(depth 2).
- Left side is
parse_primary(depth 2)- Sees
Operand(3)at index 6. - Calls
parse_operand(depth 5), consumes it, and returns3.
- Sees
parse_expression(depth 1)- Computes
3 - 3 = 0. - No more operators, so it returns
0as the final result.
- Computes
It works! But we can do better
This baseline parser works well, but it’s not optimized.
If we compile it in release mode and execute it for the test file of 1.5GB, it takes 43.87 seconds to execute on my laptop:
Step 1: Input file read in 1.189915008s
Step 2: Calculation completed in 41.876205675s
--- Summary ---
Result: 2652
Total time: 43.06795088s
While the current parser is correct, its 43-second runtime shows there is room for improvement. Our goal is to make it faster and more memory-efficient.
We will improve the parser’s performance through several key optimizations:
- Eliminate unnecessary allocations: First, we’ll change the tokenizer to avoid creating a list of tokens in memory.
- Process bytes directly: We’ll modify the parser to read raw bytes instead of string slices, reducing overhead.
- Parallelize the work: We’ll use multithreading and SIMD to perform calculations in parallel.
- Optimize file I/O: Finally, we’ll use memory-mapped files to speed up file reading.
Let’s get started.
Optimizations for speed and memory
Optimization 1: Do not allocate a Vector when tokenizing (43.1 s → 6.45 s, –85% improvement)
Let’s use cargo flamegraph to visualize the call stack of the current solution and identify areas for optimization.
cargo flamegraph --dev --bin parser
We get the following flame graph:
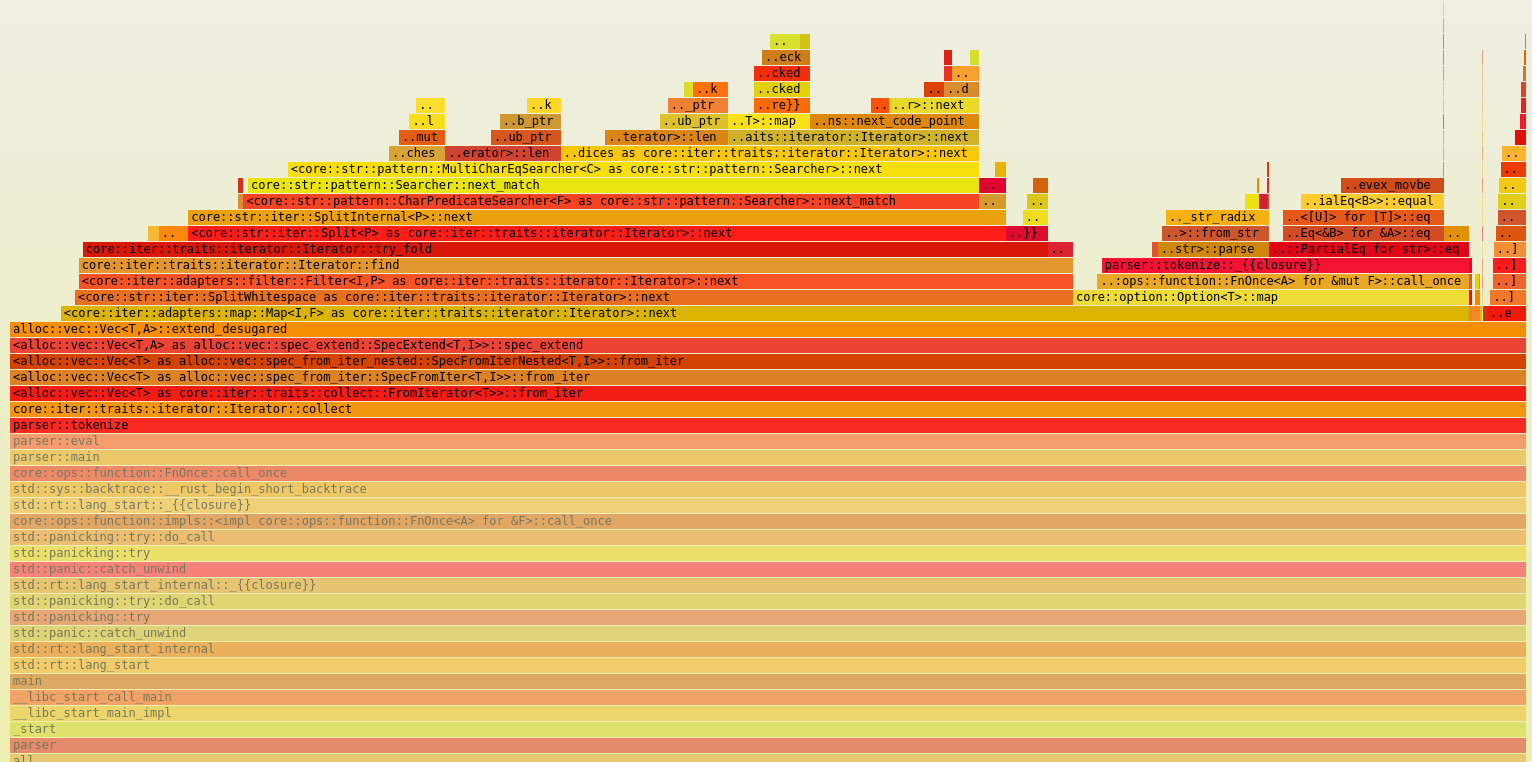
We can see that the majority of the time is spent in the tokenizer function, which reads the input string and allocates a vector of tokens.
To profile memory usage, we can use dhat to generate a profile JSON file and view it at https://nnethercote.github.io/dh_view/dh_view.html:
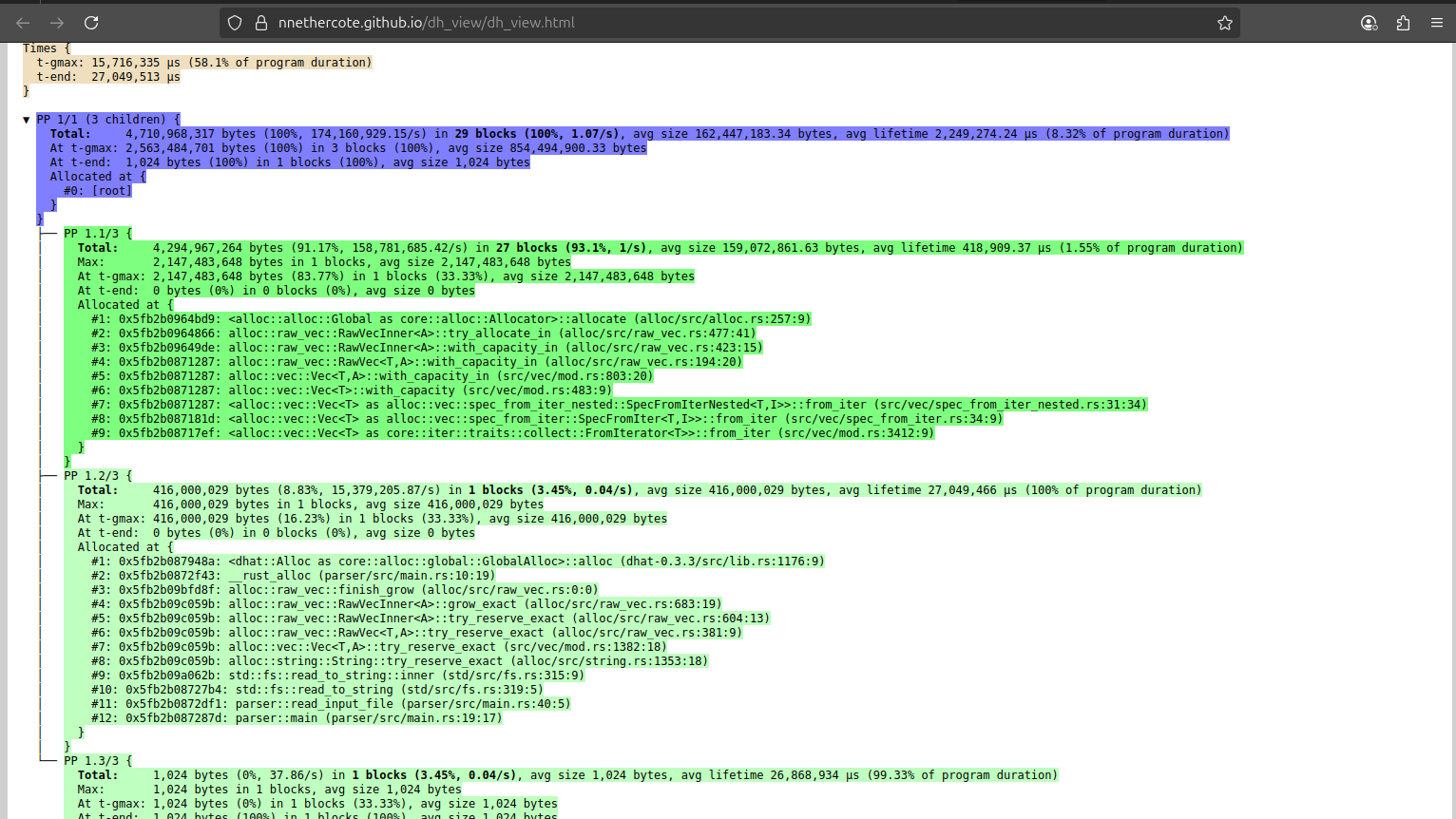
Notice how 4 GB of RAM is used just to allocate the token vector!
I made a mistake in my initial implementation. Why does the tokenize function return a vector if we’re converting it into an iterator later anyway? Let’s just return a lazy iterator directly instead of allocating a vector:
fn eval(input: &str) -> u32 {
let mut tokens = tokenize(input).peekable();
parse_expression(&mut tokens)
}
fn tokenize(input: &str) -> impl Iterator<Item = Token> + '_ {
input.split_whitespace().map(|s| match s {
"+" => Token::Plus,
"-" => Token::Minus,
"(" => Token::OpeningParenthesis,
")" => Token::ClosingParenthesis,
n => Token::Operand(n.parse().unwrap()),
})
}
If we run the parser again after this small change, the speed improves significantly:
Step 1: Input file read in 1.249408413s
Step 2: Calculation completed in 5.204344393s
--- Summary ---
Result: 2652
Total time: 6.45377661s
Wow! From 43 seconds down to just 6.45. What an improvement. A small mistake can have a huge impact on performance. Fortunately, the flamegraph pointed us straight to the bottleneck!
Optimization 2: Zero allocations — parse directly from the input bytes (6.45 s → 3.68 s, –43% improvement)
After removing the initial Vec allocation, performance improved significantly. But we can still do better.
If we analyze the flamegraph again, we notice that although we no longer allocate a vector of tokens, we’re still splitting the input string by whitespace. This iterator-based approach is a huge improvement, but there is still overhead in processing the string and creating &str slices for each token:
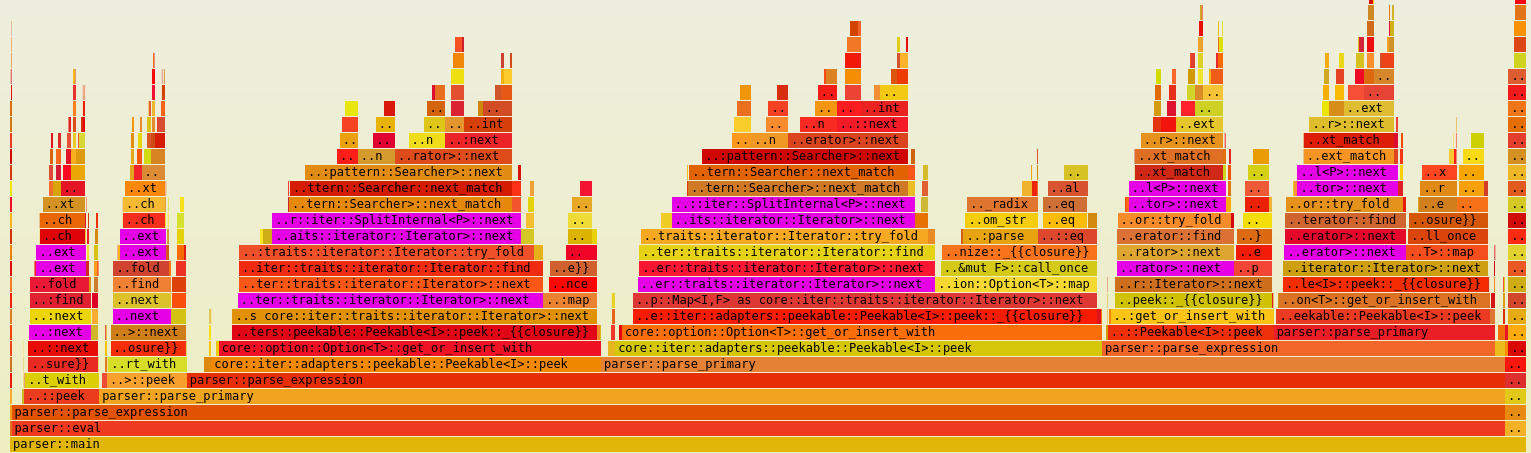
The pink/violet boxes correspond to the split_whitespace function used by our tokenizer:
fn tokenize(input: &str) -> impl Iterator<Item = Token> + '_ {
input.split_whitespace().map(|s| match s {
"+" => Token::Plus,
"-" => Token::Minus,
"(" => Token::OpeningParenthesis,
")" => Token::ClosingParenthesis,
n => Token::Operand(n.parse().unwrap()),
})
}
We’re paying a cost for each split_whitespace call, which allocates intermediate slices. This churns memory and CPU cycles.
Let’s dive deeper.
The idea: Use &[u8]
Instead of working with UTF-8 strings and &str, we can use raw bytes (&[u8]) and manually scan for digits and operators to avoid temporary string allocations.
Here is our new zero-allocation tokenizer:
fn read_input_file() -> Result<Vec<u8>> {
fs::read("data/input.txt")
}
struct Tokenizer<'a> {
input: &'a [u8],
pos: usize,
}
impl<'a> Iterator for Tokenizer<'a> {
type Item = Token;
fn next(&mut self) -> Option<Self::Item> {
if self.pos >= self.input.len() {
return None;
}
let byte = self.input[self.pos];
self.pos += 1;
let token = match byte {
b'+' => Some(Token::Plus),
b'-' => Some(Token::Minus),
b'(' => Some(Token::OpeningParenthesis),
b')' => Some(Token::ClosingParenthesis),
b'0'..=b'9' => {
let mut value = byte - b'0';
while self.pos < self.input.len() && self.input[self.pos].is_ascii_digit() {
value = 10 * value + (self.input[self.pos] - b'0');
self.pos += 1;
}
Some(Token::Operand(value))
}
other => panic!("Unexpected byte: '{}'", other as char),
};
self.pos += 1; // skip whitespace
return token;
}
}
The only heap allocation occurs when the file is read into a vector. The tokenizer operates on references to that vector of bytes and does not perform any intermediate allocations.
If we execute the program again, we get:
Step 1: Input file read in 1.212080967s
Step 2: Calculation completed in 2.471639289s
--- Summary ---
Result: 2652
Total time: 3.683753465s
A great improvement! From 6.45 to 3.68 seconds, nearly 2 seconds faster!
Optimization 3: Do not use Peekable (3.68 s → 3.21 s, –13% improvement)
The new flamegraph shows several samples related to Peekable:
core::iter::adapters::peekable::Peekable::peek::_core::iter::adapters::peekable::Peekable::peek

This is because we wrap our tokenizer in Rust’s Peekable adapter, which allows us to inspect the next token without consuming it. We initially used it for look ahead when parsing expressions like 1 + (2 - 3) to determine whether to continue parsing or return early.
However, in our use case, peek() isn’t necessary. We can restructure the algorithm to work directly with a plain iterator.
Here’s the old version:
fn parse_expression(tokens: &mut Peekable<impl Iterator<Item = Token>>) -> u32 {
let mut left = parse_primary(tokens);
while let Some(Token::Plus) | Some(Token::Minus) = tokens.peek() {
let operator = tokens.next();
let right = parse_primary(tokens);
left = match operator {
Some(Token::Plus) => left + right,
Some(Token::Minus) => left - right,
other => panic!("Expected operator, got {:?}", other),
};
}
left
}
And here’s the new version that eliminates Peekable:
fn parse_expression(tokens: &mut impl Iterator<Item = Token>) -> u32 {
let mut left = parse_primary(tokens);
while let Some(token) = tokens.next() {
if token == Token::ClosingParenthesis {
break;
}
let right = parse_primary(tokens);
left = match token {
Token::Plus => left + right,
Token::Minus => left - right,
other => panic!("Expected operator, got {:?}", other),
};
}
left
}
We replaced the peek() logic with a match on the current token. If it’s a + or -, we consume the right-hand operand and compute the result. If it’s a closing parenthesis, we break (this is an important point: we no longer manually skip the closing parenthesis after parsing a sub-expression).
Previously, with peekable, we consumed the (, parsed the sub-expression, and then had to explicitly next() again to discard the ) after the recursive call. Now, since we’re using a flat iterator, we simply let the closing ) token be returned by next(), and our while let Some(token) loop handles it. If the token is a ), we break out of the loop, and the recursive call returns.
We also simplified parse_primary in a similar way:
fn parse_primary(tokens: &mut impl Iterator<Item = Token>) -> u32 {
match tokens.next() {
Some(Token::OpeningParenthesis) => {
let val = parse_expression(tokens);
val
}
Some(Token::Operand(n)) => n as u32,
other => panic!("Expected number, got {:?}", other),
}
}
By avoiding peek() and handling the tokens linearly, we improve the performance:
Step 1: Input file read in 1.116952011s
Step 2: Calculation completed in 2.094806113s
--- Summary ---
Result: 2652
Total time: 3.21178544s
From 3.68 to 3.21 seconds. We are getting faster. Let’s continue optimizing!
Optimization 4: Multithreading and SIMD (3.21 s → 2.21 s, –31% improvement)
The next logical step is to parallelize the computation. Ideally, if we have a CPU with 8 cores, we want to split the input file into 8 equal chunks and have each core work on one chunk simultaneously. This should, in theory, make our program up to 8 times faster.
However, this is not as simple as just splitting the file into 8 equal chunks. We are bound by the rules of math and syntax, which introduce two restrictions:
- We cannot split inside parentheses. A split can only happen at the “top level” of the expression. For example, splitting
((2 + 1)| - 2)is invalid, and this applies to nested parentheses as well. - We cannot split at a
-operator. Addition is associative, meaning(a + b) + cis equivalent toa + (b + c). This property allows us to group additions freely. Subtraction, however, is not associative:(a - b) - cis not the same asa - (b - c). Splitting on a-would alter the order of operations and lead to an incorrect result.
These restrictions mean we cannot simply split the file at (total_size / 8). We need a way to find the closest valid split point (a + sign at the top level) to that ideal boundary.
To find these points, we would need to scan the entire input to identify where all current parentheses are closed. A naive scan for this would be slow, requiring a full pass over the data just to find the split points before the actual work begins. So, is this solution slower (2 passes vs 1 pass)? Not necessarily. We can make the first pass blazing fast by using SIMD.
The algorithm at a high level
Before diving into the code, let’s look at the high-level plan. The entire process is started by our parallel_eval function, which follows this data flow:
[ Input File ]
|
v
.-----------------------.
| parallel_eval |
'-----------------------'
|
| 1. Find Splits
v
.----------------------------------.
| find_best_split_indices_simd |------> [ Split Indices ]
'----------------------------------' |
| |
| 2. Create Chunks |
v |
[ Chunk 1 ] [ Chunk 2 ] ... [ Chunk N ] <--------+
| | |
| | | 3. Process in Parallel
v v v
.------------------------------------.
| Thread Pool |
| |
| eval(c1) eval(c2) ... eval(cN) |
'------------------------------------'
|
| 4. Collect Results
v
[ Result 1, Result 2, ... Result N ]
|
| 5. Sum Results
v
[ Final Answer ]
What is SIMD?
SIMD stands for Single Instruction, Multiple Data. It’s a powerful feature built into modern CPUs. At its core, SIMD allows the CPU to perform the same operation on multiple pieces of data at the same time, with a single instruction.
Consider a cashier at a grocery store. A traditional CPU core operates like a cashier scanning items one by one. This is a scalar operation, where one instruction processes one piece of data.
Scalar Operation (One by one)
Instruction: Is this byte '+'?
|
V
[ H | e | l | l | o | | + | | W | o | r | l | d ]
^--- Processed sequentially --->
A SIMD-enabled CPU is like a cashier with a wide scanner that can read the barcodes of an entire row of items in the cart simultaneously. This is a vector operation.
SIMD Operation (All at once)
Instruction: For all 64 of these bytes, tell me which ones are '+'?
|
V
[ H | e | l | l | o | | + | | W | o | r | l | d | ... (up to 64 bytes) ]
[ 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ... (result mask) ]
\_______________________________________________________________________/
Processed in a single cycle
For repetitive tasks, such as searching for a specific character in a long string, the performance gain is great.
SIMD example: Finding +
In our project, we need to locate all + characters.
The Scalar Way: Without SIMD, we would need a simple for loop to check every single byte:
let mut positions = Vec::new();
for (i, &byte) in input.iter().enumerate() {
if byte == b'+' {
positions.push(i);
}
}
This approach is simple and correct, but for a 1.5GB file like ours, this loop would execute 1.5 billion times.
The SIMD Way: With SIMD (specifically, using AVX-512 instructions), the process is different:
- Load: We load a big chunk of our input string (64 bytes at a time) into a wide 512-bit CPU register.
- Compare: We use a single instruction (
_mm512_cmpeq_epi8_mask) to compare all 64 bytes in our register against a template register that contains 64 copies of the+character. - Get Mask: The CPU returns a single 64-bit integer (
u64) as a result. This is a bitmask. If the 5th bit of this integer is1, it indicates that the 5th byte of our input chunk was a+.
In a single instruction, we have done the work of 64 loop iterations. While SIMD requires more complex code, the performance gains are worth it.
The Code
Here are the two key functions that implement our parallel strategy: parallel_eval orchestrates the process, and find_best_split_indices_simd uses SIMD to find the valid split points.
fn parallel_eval(input: &[u8], num_threads: usize) -> i64 {
if num_threads <= 1 || input.len() < 1000 {
return eval(input);
}
// 1. Find the best places to split the input.
let split_indices = unsafe { find_best_split_indices_simd(input, num_threads - 1) };
if split_indices.is_empty() {
return eval(input);
}
// 2. Create the chunks based on the indices.
let mut chunks = Vec::with_capacity(num_threads);
let mut last_idx = 0;
for &idx in &split_indices {
// Slice from the last index to just before the operator's space.
chunks.push(&input[last_idx..idx - 1]);
// The next chunk starts after the operator and its space.
last_idx = idx + 2;
}
chunks.push(&input[last_idx..]);
// 3. Process all chunks in parallel with Rayon.
let chunk_results: Vec<i64> = chunks.par_iter().map(|&chunk| eval(chunk)).collect();
// 4. Since we only split on '+', the final result is the sum of all parts.
chunk_results.into_iter().sum()
}
#[cfg(target_arch = "x86_64")]
#[target_feature(enable = "avx512f")]
#[target_feature(enable = "avx512bw")]
unsafe fn find_best_split_indices_simd(input: &[u8], num_splits: usize) -> Vec<usize> {
// Explanation of this function in the next section.
let mut final_indices = Vec::with_capacity(num_splits);
if num_splits == 0 {
return final_indices;
}
let chunk_size = input.len() / (num_splits + 1);
let mut target_idx = 1;
let mut last_op_at_depth_zero = 0;
let mut depth: i32 = 0;
let mut i = 0;
let len = input.len();
let open_parens = _mm512_set1_epi8(b'(' as i8);
let close_parens = _mm512_set1_epi8(b')' as i8);
let pluses = _mm512_set1_epi8(b'+' as i8);
'outer: while i + 64 <= len {
if final_indices.len() >= num_splits {
break;
}
let chunk = _mm512_loadu_si512(input.as_ptr().add(i) as *const _);
let open_mask = _mm512_cmpeq_epi8_mask(chunk, open_parens);
let close_mask = _mm512_cmpeq_epi8_mask(chunk, close_parens);
let plus_mask = _mm512_cmpeq_epi8_mask(chunk, pluses);
let mut all_interesting_mask = open_mask | close_mask | plus_mask;
while all_interesting_mask != 0 {
let j = all_interesting_mask.trailing_zeros() as usize;
let current_idx = i + j;
if (open_mask >> j) & 1 == 1 {
depth += 1;
} else if (close_mask >> j) & 1 == 1 {
depth -= 1;
} else { // Is a '+' operator
if depth == 0 {
last_op_at_depth_zero = current_idx;
let ideal_pos = target_idx * chunk_size;
if current_idx >= ideal_pos {
final_indices.push(current_idx);
target_idx += 1;
if final_indices.len() >= num_splits {
break 'outer;
}
}
}
}
all_interesting_mask &= all_interesting_mask - 1;
}
i += 64;
}
// ... scalar remainder and fill logic ...
while i < len && final_indices.len() < num_splits {
let char_byte = *input.get_unchecked(i);
if char_byte == b'(' { depth += 1; }
else if char_byte == b')' { depth -= 1; }
else if char_byte == b'+' && depth == 0 {
last_op_at_depth_zero = i;
let ideal_pos = target_idx * chunk_size;
if i >= ideal_pos {
final_indices.push(i);
target_idx += 1;
}
}
i += 1;
}
while final_indices.len() < num_splits && last_op_at_depth_zero > 0 {
final_indices.push(last_op_at_depth_zero);
}
final_indices
}
Algorithm Breakdown: find_best_split_indices_simd
This function’s purpose is to identify the optimal + signs for splitting.
Step 1: The SIMD Scan
The code enters a main loop, processing the input in 64-byte chunks. Within this loop, it uses _mm512_cmpeq_epi8_mask to generate bitmasks. This instruction compares all 64 bytes of the current chunk against a target character and returns a 64-bit integer (u64) where the N-th bit is 1 if the N-th byte was a match.
Step 2: The serial scan
Next, we combine these masks and iterate only through the “interesting” bits. This is a key step:
let mut all_interesting_mask = open_mask | close_mask | plus_mask; // This means we are looking for '(', ')' and '+' characters.
while all_interesting_mask != 0 {
let j = all_interesting_mask.trailing_zeros() as usize; // j is the index of the next found interesting character.
let current_idx = i + j; // + j because the mask is a u64 little endian, so trailing zeros are the leading 0 in reality
if (open_mask >> j) & 1 == 1 { // If that char is a '(' we increase the depth (we enter in a sub expression)
depth += 1;
} else if (close_mask >> j) & 1 == 1 { // If that char is a ')' we decrease the depth (we exit from a sub expression)
depth -= 1;
} else {
if depth == 0 { // If the depth is 0, we are at a top level, outside of parentheses. And it is a '+' sign.
last_op_at_depth_zero = current_idx;
if current_idx >= ideal_pos { // If we have reached the ideal position (chunk / NUM_THREADS). So we add this '+' sign to the splitting indices.
final_indices.push(current_idx);
target_idx += 1;
if final_indices.len() >= num_splits {
break 'outer;
}
}
}
}
all_interesting_mask &= all_interesting_mask - 1; // Clears the lowest set 1 bit from the mask, as we have processed it already
}
This loop does not run 64 times. It only runs for the number of set bits in all_interesting_mask. To understand how it processes characters from left-to-right, we need to look at two key details:
-
trailing_zeros()and Little-Endian: While you might assumetrailing_zerosstarts from the end of the string, it’s actually the opposite. Modern x86-64 CPUs are little-endian. When a block of memory is loaded into a large integer register, the first byte in memory (e.g.,chunk[0]) becomes the least significant byte (LSB) of the integer. Thetrailing_zeros()instruction counts from this LSB, meaning it always finds the set bit corresponding to the character with the lowest index in our chunk.Memory (Bytes in a chunk): Byte Index: 0 1 2 3 ... 63 Content: '(' '1' '+' '2' ... 'X' | | Load into a 64-bit integer v Resulting u64 Bitmask: Bit Position: 63 ... 3 2 1 0 <-- LSB (The "trailing" end) Corresponds to: 'X' ... '2' '+' '1' '('As you can see,
trailing_zerosstarts from the right of the integer, which corresponds to the left of our string chunk. -
if (open_mask >> j) & 1 == 1 {: This is just to check if there is an open parenthesis at positionj. If so, we increment our counterdepth. -
all_interesting_mask &= all_interesting_mask - 1: This is a trick that clears the lowest set 1 bit we just found. On the next iteration,trailing_zerosfinds the new lowest set bit, which corresponds to the character at the next lowest index.
This combination allows us to visit every interesting character in the correct, forward order, but without a slow byte-by-byte scan. Inside the loop, we just update our depth counter to know if we are at a top level position, and if so, we check if we can add a splitting point.
Full example
Let’s trace the entire flow with a small, concrete example:
- Input String:
(1-2) + (3-4) + (5-6)(Length is 23 bytes) - Goal: Find 1 split point (
num_splits = 1) to create 2 chunks. - Ideal Split Position:
1 * (23 / 2) = 11. We are looking for the first+at depth 0 at or after byte 11.
Part 1: find_best_split_indices_simd runs
The function will scan the input to find the best split point.
Input: ( 1 - 2 ) + ( 3 - 4 ) + ( 5 - 6 )
Index: 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2
1 1 1 1 1 1 1 1 1 1 2 2 2
Depth: 1 1 1 1 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 0 0
Ideal Split -> ^
- The code starts scanning. It finds the first
+at index7. - It checks the depth. The
(at index 0 increased depth to 1, and the)at index 5 decreased it back to 0. So, at index 7,depth == 0. - It checks the splitting logic:
is current_idx (7) >= ideal_pos (11)?The answer is No. The code continues scanning. - The code finds the next
+at index15. - It checks the depth. The
(at index 9 and)at index 13 have kept the depth at 0. - It checks the splitting logic:
is current_idx (15) >= ideal_pos (11)?The answer is Yes! - Action: The code pushes
15intofinal_indicesand immediately breaks out of all loops because it has found the 1 split it was looking for. - The function returns
[15].
Part 2: parallel_eval receives the result
split_indicesis now[15].- The
forloop runs once for the index15.- It creates the first chunk by slicing from
0to15 - 1 = 14. The chunk is(1-2) + (3-4). - It updates
last_idxto15 + 2 = 17.
- It creates the first chunk by slicing from
-
The loop finishes. It creates the final chunk by slicing from
17to the end. The chunk is(5-6).Original: (1-2) + (3-4) + (5-6) <-- chunk 1 --> <-- chunk 2 --> Split Index: ^ (15) - The two chunks,
(1-2) + (3-4)and(5-6), are sent to the Rayon thread pool. - Thread 1 gets
(1-2) + (3-4), callseval, and gets the result-2. - Thread 2 gets
(5-6), callseval, and gets the result-1. collect()gathers the results into a vector:[-2, -1].- Finally,
sum()adds them together:-2 + -1 = -3.
The final answer is -3, which is correct. The entire process worked perfectly.
Result
In summary, by using SIMD, we can perform an initial, extremely fast pass to identify optimal split points in the input, and then process each chunk in parallel. I believe a similar technique is employed by the popular simdjson library.
I executed the code on my Surface laptop, and here are the results:
Step 1: Input file read in 1.199915008s
Step 2: Calculation completed in 1.010507822s
--- Summary ---
Result: 2652
Total time: 2.210422830s
From 3.21 to 2.21 seconds. 1 second faster, for an already optimized program. Good!
Optimization 5: Memory-Mapped I/O (2.21 s → 0.98 s, –56% improvement)
After profiling the memory usage of our parallel solution, we can see that we’re still allocating a very large buffer on the heap to hold the entire file’s contents.
mmap (memory-mapped files) can be more efficient than standard file I/O because it avoids extra copying from kernel to user space, and allows the operating system to manage memory for us.
When I initially tried mmap with the single-threaded version of the code, the performance gain was negligible. However, now that our program is multithreaded, let’s re-evaluate its impact.
Kernel Space vs. User Space
- Kernel space: The privileged area where the operating system runs, managing hardware, I/O, and the page cache.
- User space: The unprivileged area where our application code executes, including your heap buffers, stacks, and other program data.
- Page cache: A kernel-managed buffer that temporarily stores file data in memory to speed up subsequent access.
Cost of fs::read
- Double Memory Footprint
[ Disk ] → [ Page Cache ] (1.5 GB) → [ Heap Vec] (1.5 GB) This process involves loading the file into kernel space and then copying it to user space.
- False Sharing Contention Modern CPUs transfer data between main memory and CPU caches in 64-byte blocks called “cache lines.” False sharing occurs when multiple threads access different variables that happen to reside on the same cache line. If one thread modifies its variable, the entire cache line is invalidated for all other threads, forcing them to re-fetch it from memory even though their own data hasn’t changed.
// Thread 1 writes to data at byte 8 // Thread 2 writes to data at byte 40 // Both bytes are in the same 64-byte cache line (0-63). // The cache line "bounces" between the cores, causing delays.With a single large
Vec, the boundaries of the chunks processed by each thread could easily fall in a way that causes this contention.
mmap improvement
Instead of reading the entire file into a Vec, we can map it directly into memory with mmap. This gives us:
use memmap2::Mmap;
fn read_input_file() -> std::io::Result<Mmap> {
let file = File::open("data/input.txt")?;
unsafe { Mmap::map(&file) }
}
This approach avoids the extra copy performed by fs::read and does not allocate the file’s content in user space memory.
[ Disk ] → [ Page Cache (1.5 GB) ] ↔ [ mmap view in user space ]
I also think it is faster because we don’t have false sharing with mmap. It hands us the file in 4 KB pages. Threads get whole pages:
Thread 1 works on data starting at Page 0 (byte 0)
Thread 2 works on data starting at Page N (byte N*4096)
Since pages (4 KB) are much larger than cache lines (64 B), threads operate on memory regions that are physically far apart, preventing them from contending over the same cache lines. I’m not entirely certain about this, but it’s my conclusion after reading a lot about the topic and consulting various LLM models.
Code Changes
The change is minimal. The read_input_file function now returns an Mmap object, which is passed directly to the parallel_eval function. This allows the operating system to efficiently map the file directly into our process memory on demand:
use memmap2::Mmap;
fn read_input_file() -> Result<Mmap> {
let file = File::open("data/input.txt")?;
unsafe { Mmap::map(&file) }
}
fn main() -> Result<()> {
let mmap = read_input_file()?;
let result = parallel_eval(&mmap, NUM_THREADS);
println!("Result: {}", result);
Ok(())
}
Performance Results
Step 1: Input file read in 18.8 µs
Step 2: Calculation completed in 981.2 ms
**Total time:** 981.3 ms
From 2.21s to 981ms. Less than a second!!
Conclusion
YOU CAN FIND THE FULL CODE ON: https://github.com/RPallas92/math_parser
We started with a simple math parser that took 43 seconds to run. By making a series of changes, we made it run in under one second. Here is a summary of what we did:
- Stopped creating a list of all tokens at once. Instead of reading the whole file and creating a big list of tokens, we processed them one by one. This was the biggest improvement, bringing the time down from 43 to 6.4 seconds. (To be honest I made this mistake in purpose just to see the difference).
- Worked with bytes instead of text. Instead of treating the input as text, we worked with the raw bytes. This avoided extra work and brought the time down to 3.7 seconds.
- Simplified the code by removing
Peekable. We changed the logic to avoid peeking at the next token, which made the code faster, reducing the time to 3.2 seconds. - Used multiple threads and modern CPU features. We used Rayon to run calculations in parallel and SIMD to find split points faster. This brought the time down to 2.2 seconds.
- Used memory-mapped files. Instead of reading the file into memory ourselves, we let the operating system handle it. This was the final optimization, bringing the time down to just 0.98 seconds.
If you have any corrections or comments, please contact me on LinkedIn or via email. Thank you very much for reading! « Pingora async runtime and threading model
Related Posts

Ricardo Pallas
λ Software Engineer
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0









































