Deep Learning Is Applied Topology

When I think about AI, I think about topology.

Topology is a big scary math word that basically means 'the study of surfaces'. Imagine you had a surface made of play-doh. You could bend it, or twist it, or stretch it. But as long as you don't rip the play-doh up, or poke a hole through it, you can define certain properties that would remain true regardless of the deformation you apply. Here's an example. Let's say I flatten out my play-doh and then draw a circle on it. I could rotate it, or bend it, or twist it, or whatever. And my circle will change shape, for sure. But my circle will never magically become a line, nor will it suddenly become two circles, nor will it ever cross over itself. This is topology in a nutshell.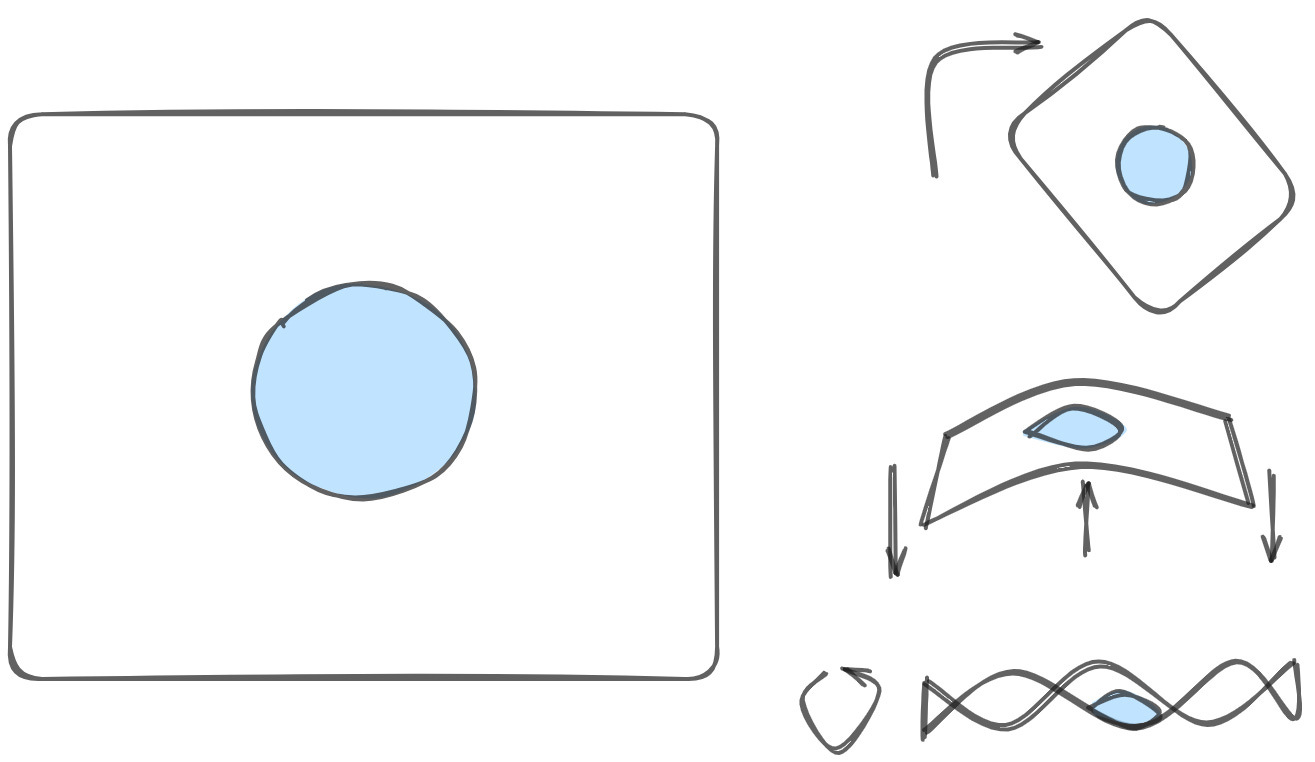

Topology shows up in all sorts of places. For example, data science.

Let's say you had a bunch of data that you wanted to classify. A lot of classification problems are equivalent to being able to cleanly separate data with a line. But when you go to plot the data on a 2D plane, it's just…kinda messy. There's no obvious line that you could draw on your plane to neatly separate the data. Does that mean that the data cannot be classified? Not necessarily! You can apply the same kinds of topological deformations to your plane, and maybe you'll find a way to separate the data.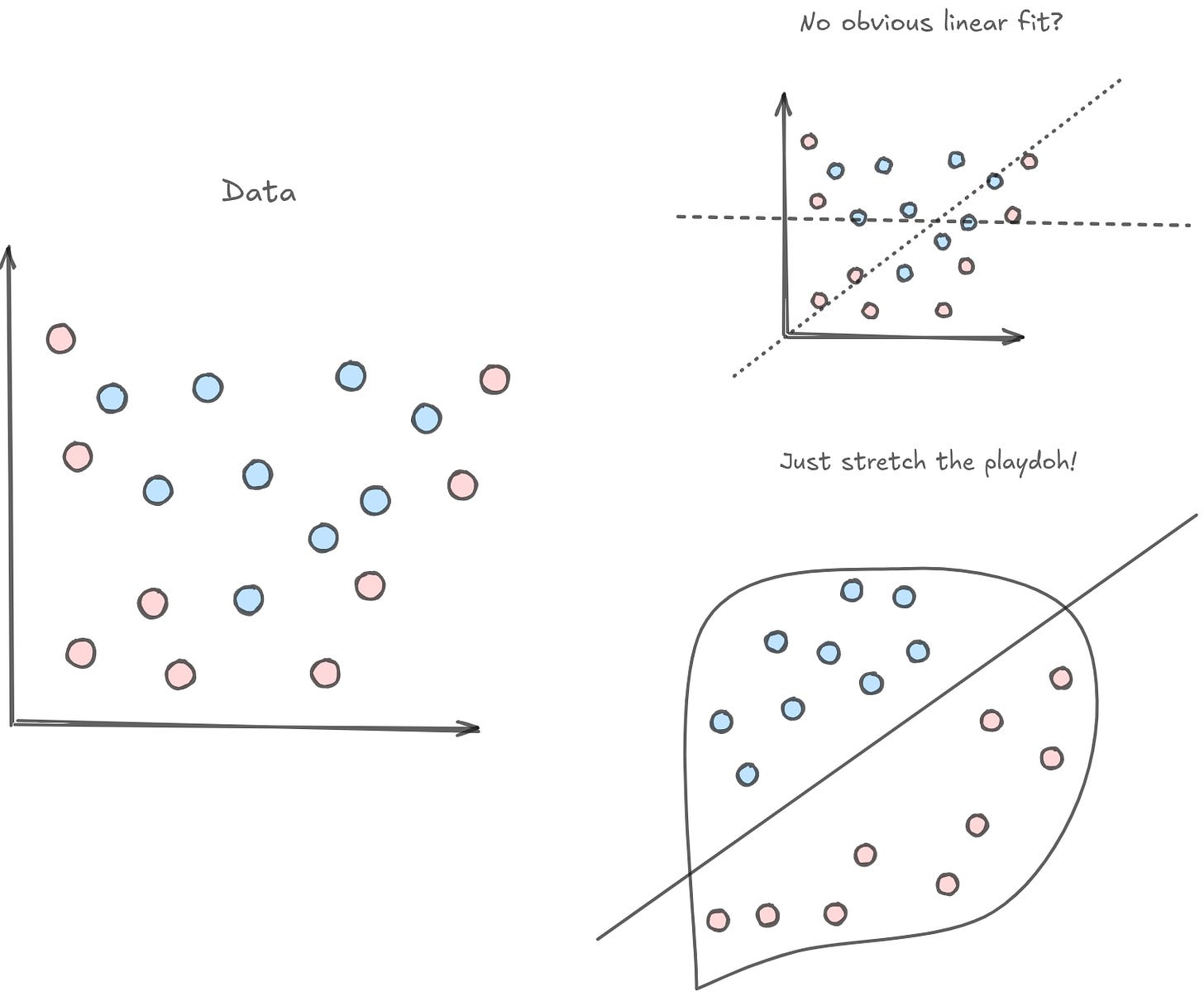

This sort of spatial manipulation is at the core of deep learning. People say that a neural network is basically just a stack of linear algebra. Well, that's more or less correct! Linear algebra is really closely tied to the manipulation of surfaces. Matrices themselves are transformations of geometric surfaces. So you can think of a stack of matrix multiplications in topological terms.

This is not a new idea — Chris Olah (one of the founders of Anthropic) wrote about deep learning manifolds back in 2014.

There are a variety of different kinds of layers used in neural networks. We will talk about tanh layers for a concrete example. A tanh layer — tanh(Wx+b) — consists of:

• A linear transformation by the “weight” matrix W

• A translation by the vector b

• Point-wise application of tanh.

We can visualize this as a continuous transformation, as follows:

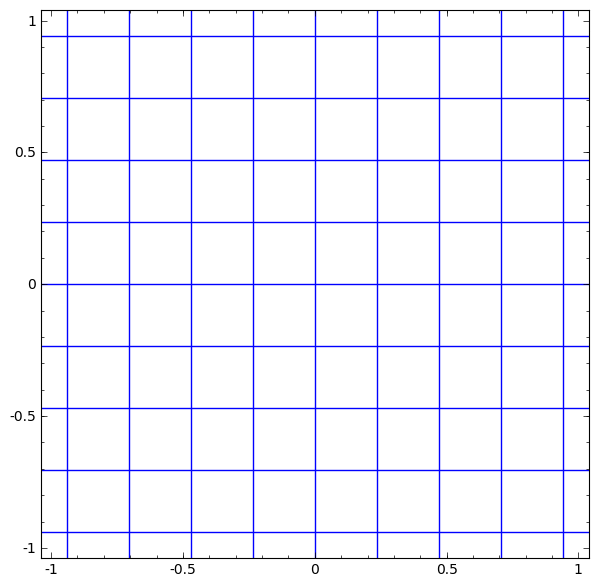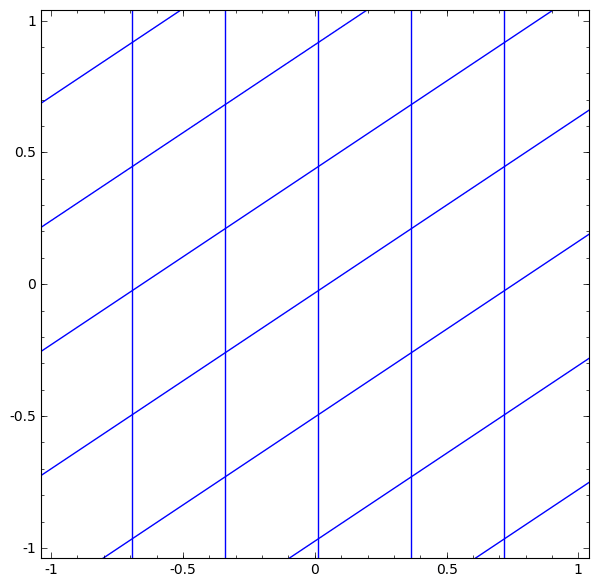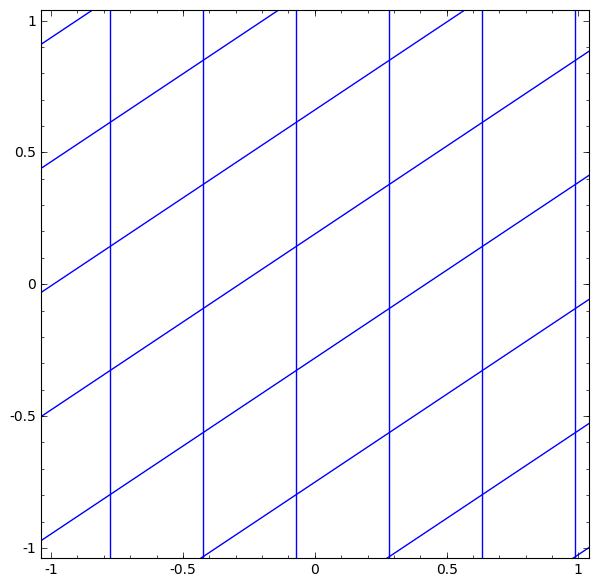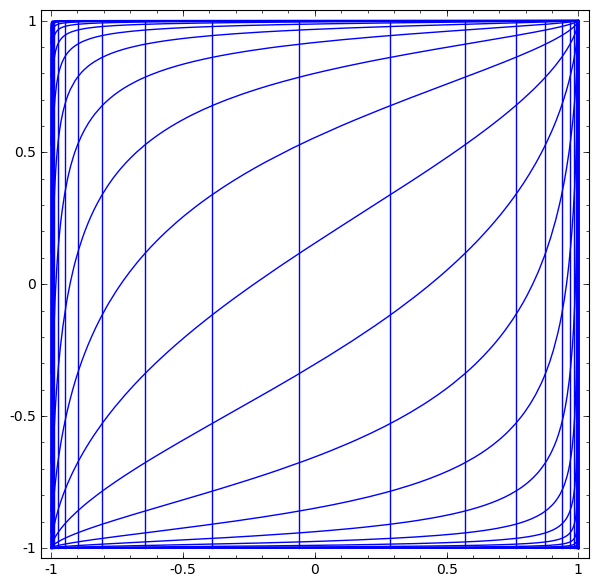
The gif above goes through each part of the neural network transformation step by step. First there is a linear transformation — that's the part where we go from a square grid to a rhomboid grid, which is represented by a matrix multiplication. Then there's the translation, where we move the grid around. That's just adding or subtracting a vector b. And finally, there's the tanh. That's where we warp the surface.

It turns out that if you stack a bunch of these kinds of transformations on top of each other, you can find ways to separate out some pretty complicated datasets.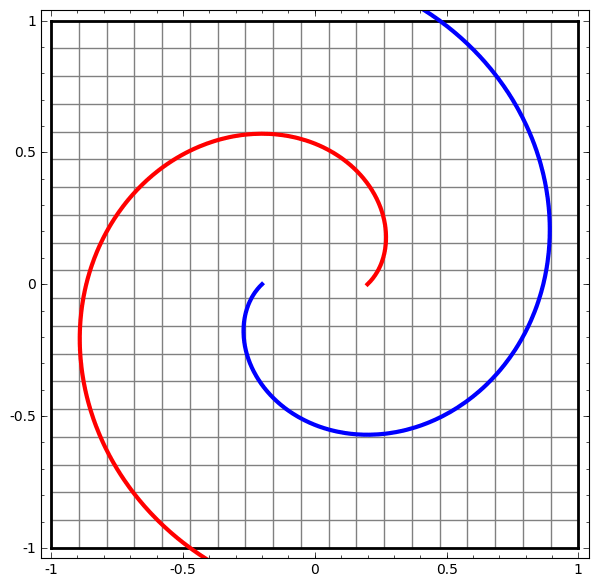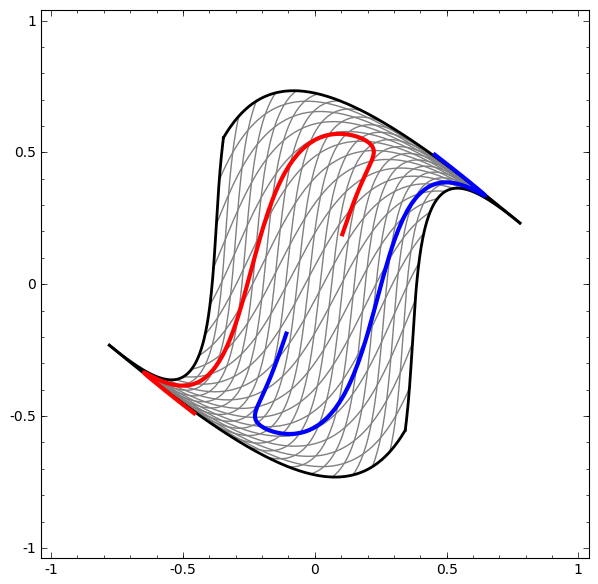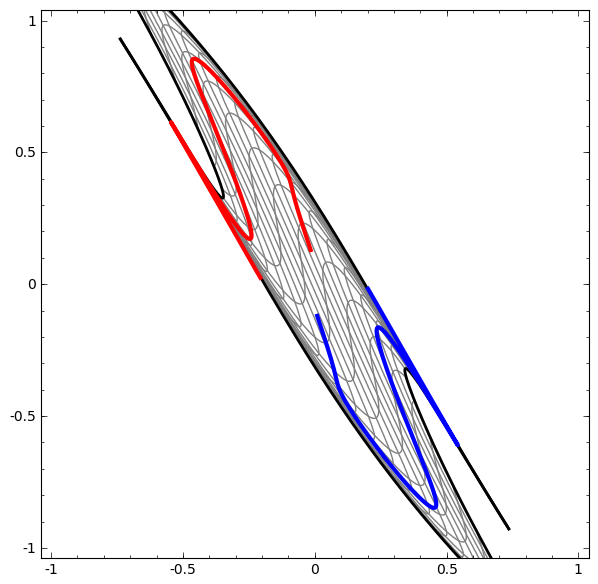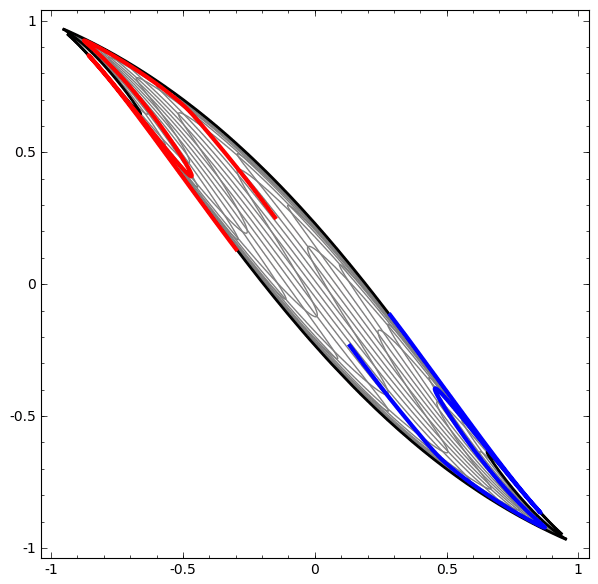

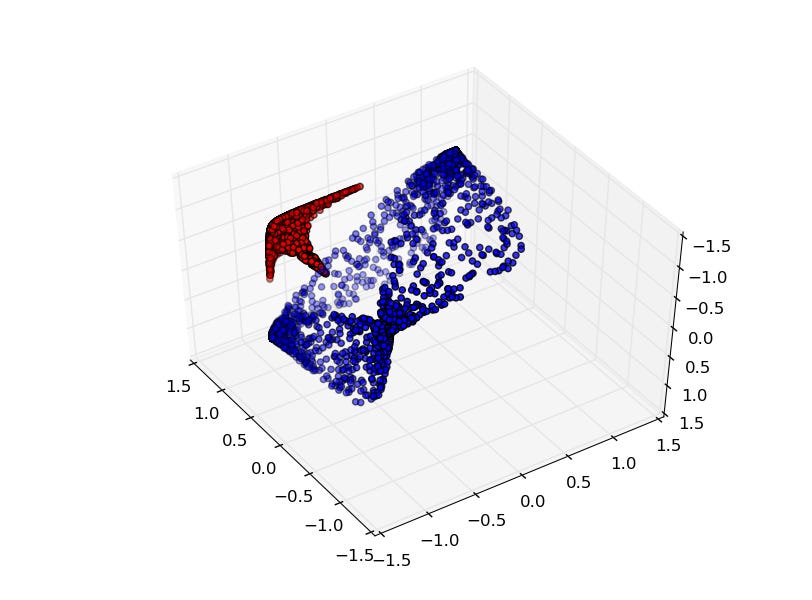
But, wait, what about things that you can't just stretch your way out of? If I have a dataset with a bunch of points in a circle surrounded by other points, what then?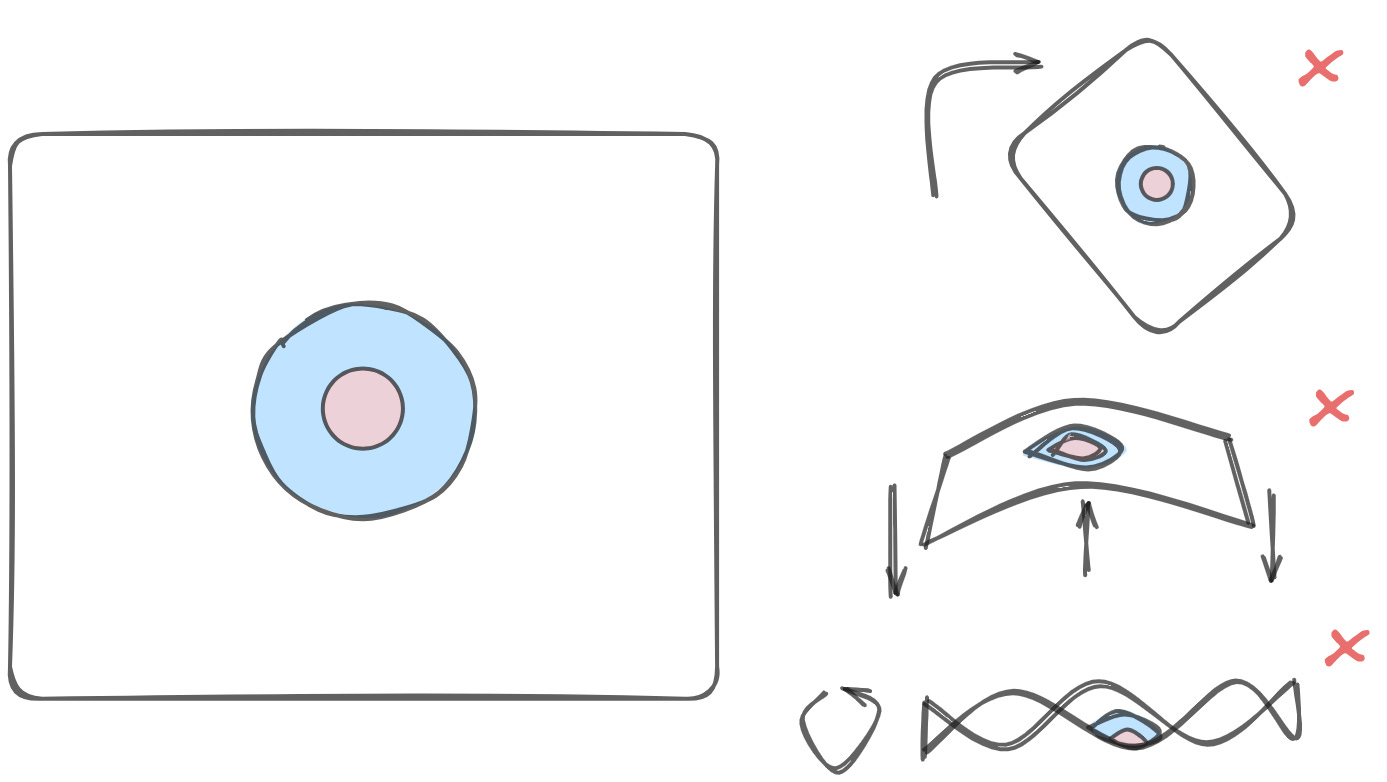

The rules of topology are ironclad — there is no way to cleanly separate these two circles with a single line. But again, that doesn't mean that the data is not separable at all. In such cases, you need to take a lesson from your neighborhood stoner and, like, move to a higher dimension, man.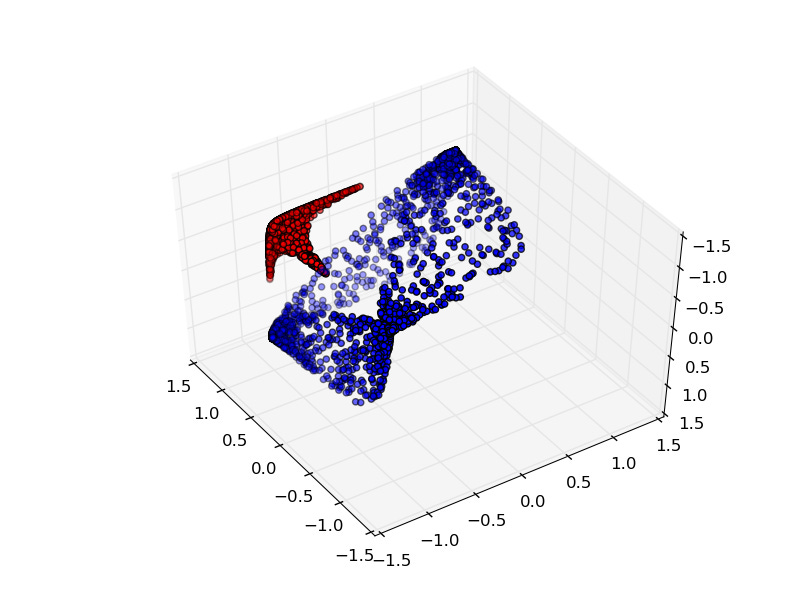

In general, things that are impossible to separate in lower dimensions can be trivial to separate in higher dimensions. Humans obviously spatially reason in three dimensions, but a neural network can “think” in arbitrarily large dimensions. So, it stands to reason, a neural network can separate all sorts of data, even data that isn't immediately obviously separable except in the sort of fuzzy way that only humans can do.

One way to think about neural networks, especially really large neural networks, is that they are topology generators. That is, they will take in a set of data and figure out a topology where the data has certain properties. Those properties are in turn defined by the loss function. If you are trying to solve some kind of categorization task, your model will learn a topology where all the dogs are in one part of the space, and all of the cats are in some other part of the space. If you are trying to learn a translation task — say, English to Spanish, or Images to Text — your model will learn a topology where bread is close to pan, or where that picture of a cat is close to the word cat. And if you are trying to learn to predict what the next token is in a sequence, your model will learn a topology where tokens are grouped by their usage. The data all lives on a high-dimensional, semantically relevant manifold. And developing the manifold is exactly equivalent to figuring out how to represent the dataset semantically.

I'm personally pretty convinced that, in a high enough dimensional space, this is indistinguishable from reasoning.

Here's a philosophical question: are topologies created or discovered? You could say that these neural nets are not really creating topologies. The topologies just, like, exist abstractly already, as a fundamental property of the data we're looking at.

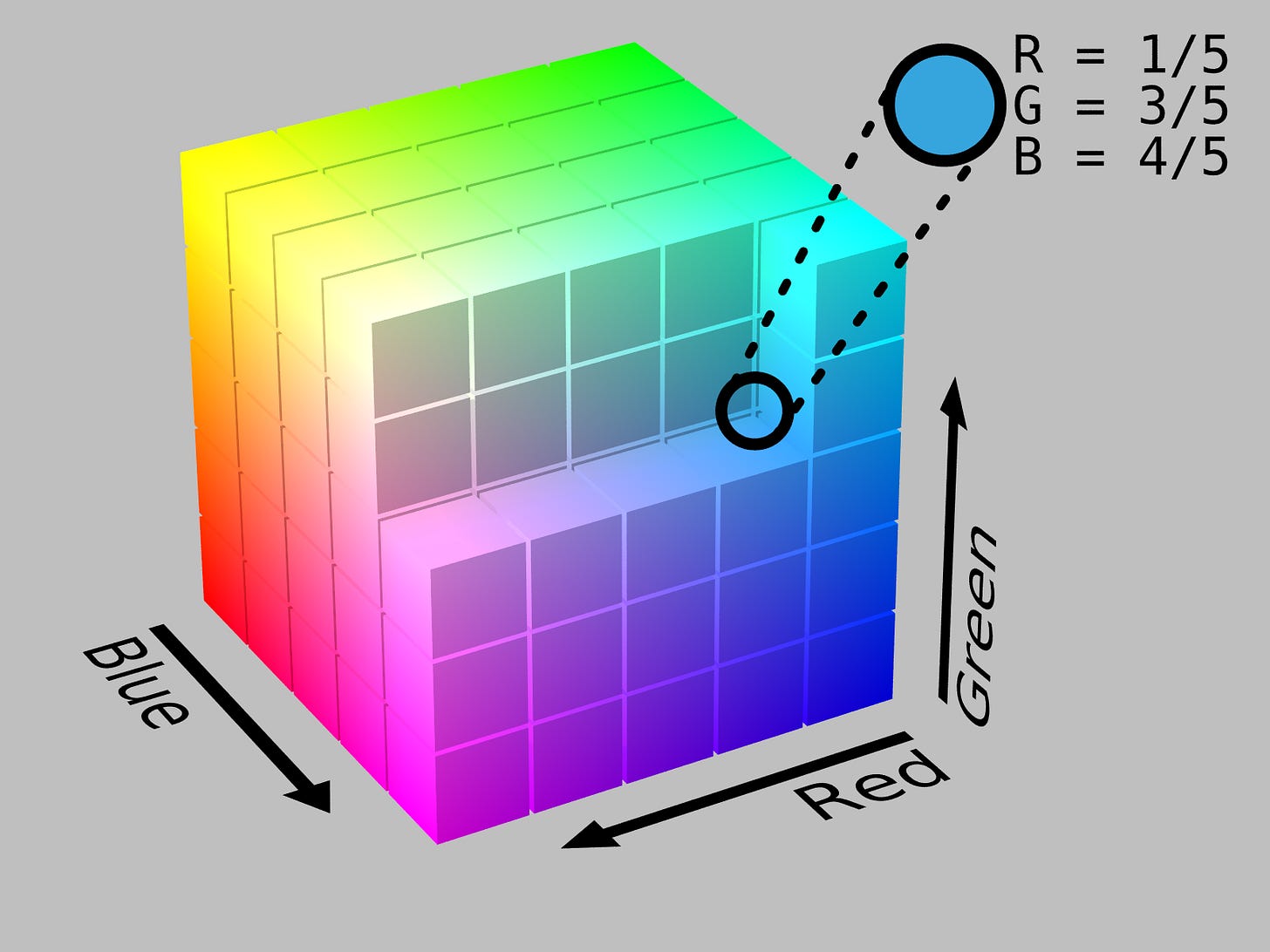
There's some trivial sense in which this is obviously true. For example, think about colors. Imagine you have two RGB vectors that represent colors — [128, 0, 0] and [0, 0, 128], representing red and blue respectively. If you wanted to make purple, what would you do?

You'd add them together.

There isn't anything special about red-green-blue in specific; you could just as easily represent the space of colors on any 3-axis plot. But the dimensionality of color, the way we think about which colors are similar to each other, the way we mix colors together to create new colors — all of that is innate to the data. "Colors" live on a manifold, one that exists in the abstract.

Images also live on a manifold. We know that images can be represented as a bunch of numbers of size Height x Width x 3, representing a grid of RGB pixel values. Well, you can flatten all those numbers out into a vector. Now you can think of any image as a point in some high dimensional space. That in turn means that you can construct a topology of every image of a certain size. There will be a region of that space with all of the images that look roughly like Brad Pitt eating a sandwich. Every direction that you move in will represent a change of a single pixel. You can walk this manifold, changing pixel by pixel until you end up at the Mona Lisa.

Most of the space is just noise, of course. And it's not particularly useful to group things by their pixel similarity. But this is where we go back to neural networks. A deep neural network can take this surface of images, and stretch it and bend it and twist it until all of the images we care about are close together and all of the noise is far away.

More generally, the model is able to take arbitrary information and put it onto a topology. Under the hood, the model is storing all of this information in a sort of universal mathematical representation: an embedding vector. That is to say, the text, or images, or whatever else are all internally represented as lists of numbers. This is really powerful. Each embedding vector is tied to a concept, but is also a mathematical construct, literally points in space. If the model learns a well formed topology, you can do mathematical operations on your conceptual data. For example, the famous "king" - "man" + "woman" = "queen" example.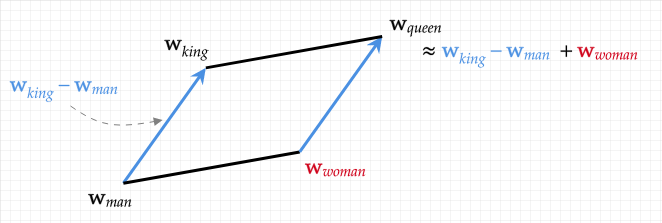

Each of these words is just a point in a high dimensional representational space.

Images obviously live on a manifold. It turns out words do too. Is there anything that doesn't live on a manifold?

No. Everything lives on a manifold.

There is a topology that measures the size and shape of different kinds of furniture, where chairs are all close to each other and far from the tables. There is a topology that represents weather conditions in Nepal, which probably gets used by JaneStreet to do commodities pricing. There is a topology that compares the smells associated with different emotions. Is this a useful topology? Who knows.

But this all points to another way to think about neural networks: they are universal topology discoverers. This leads to some useful ideas.

There is some sense in which reasoning itself lives on a manifold. That is, you can imagine a hypothetical manifold where all of the good reasoning is clustered on one side of some topological space, and all of the 'bad' reasoning is clustered on the other side of the space. We may not be able to define 'good' and 'bad' in strict mathematical terms, but as long as we can separate good from bad we can train a neural network to sort out the topology for us.

And in fact, that is exactly what all the big players — Google / Anthropic / OAI / DeepSeek — are doing.

The general consensus in the AI world is that we've more or less extracted everything we were going to get out of pure language statistics. Most of the LLMs are trained on trillions of tokens; there may be some additional juice to squeeze by training on quadrillions of tokens, but it's not a lot. Put a slightly different way, learning to predict the next token in a sequence is not going to get you to reasoning, it's going to make you really good at predicting the next token in a sequence, and we've already more or less hit that asymptote.

But it turns out that next-word-prediction is like reasoning. You can construct a topology where next-word-prediction is in one part of the space, and you want to move towards question-answering reasoning. Instruction tuning and RLHF are ways to move from the next-word-prediction part of the reasoning manifold towards the QA part of the reasoning manifold. And Chain of Thought reasoning explicitly moves towards, well, the 'reasoning' part of the reasoning manifold.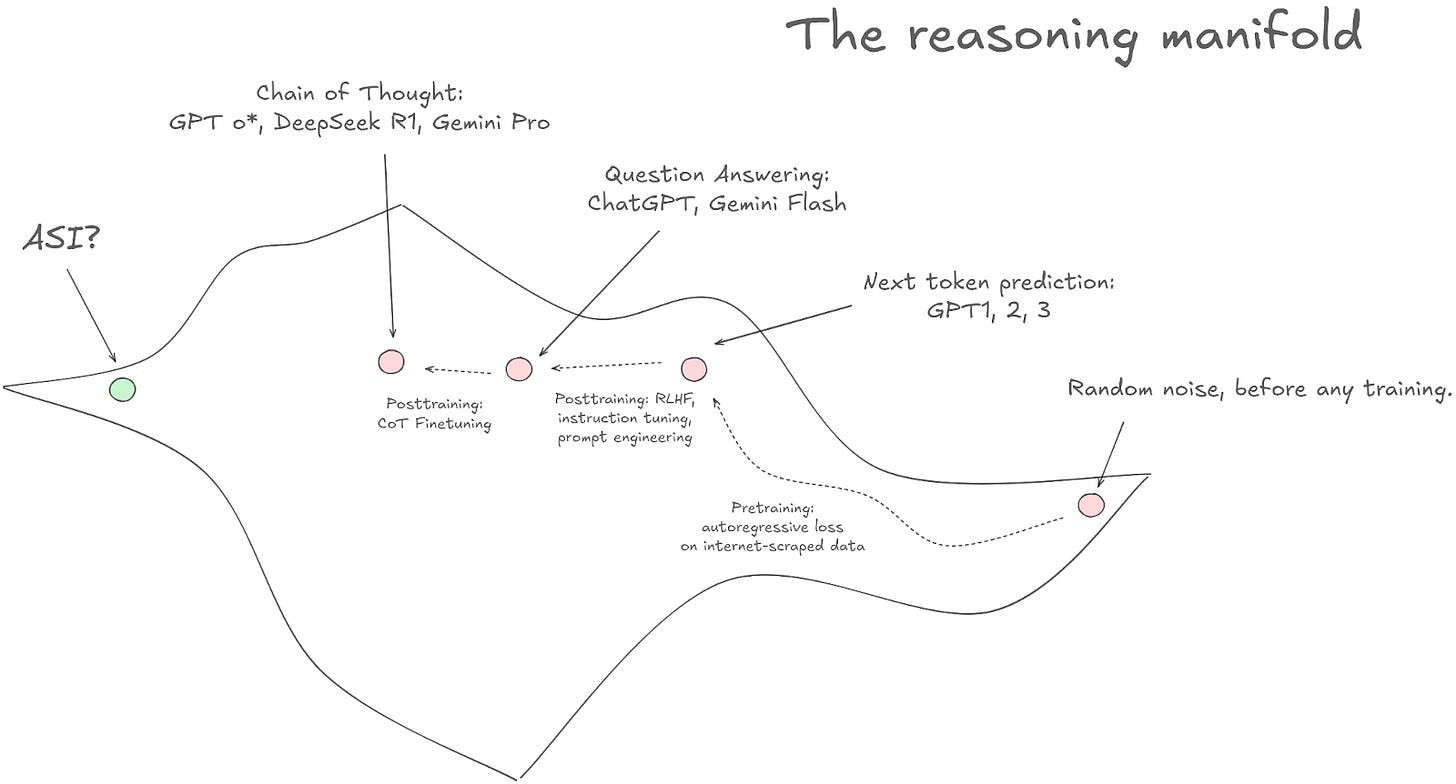

That last step says "Chain of Thought Finetuning." That is where most of the value proposition is in AI training right now. The basic idea is straightforward. You know how, when you use a model like o3 or Gemini 2.5, there is a part of the prompt that says "Thinking…" that you can click into to see the 'thought process' of the LLM? That's called a 'reasoning trace'.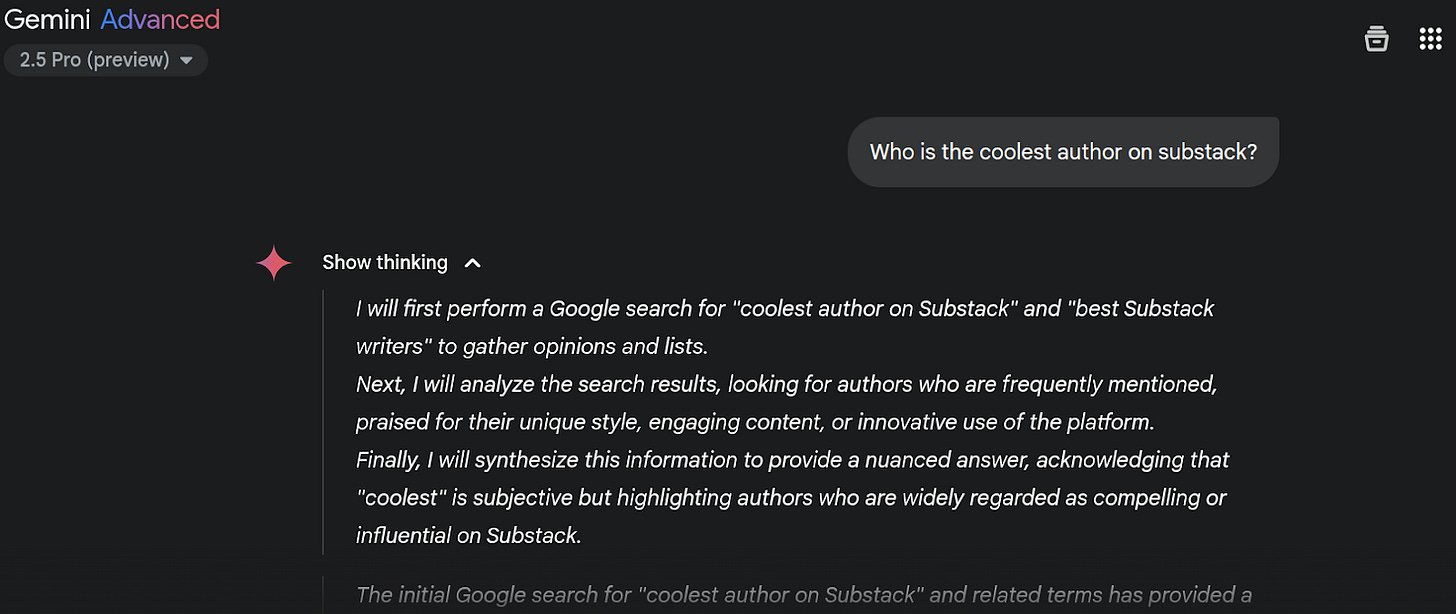

If you run queries on LLMs a whole bunch of times, you will be able to find some reasoning traces that are good, and some that are bad. For example, the one above is bad, it should say something like:

Let's say you run a million such queries, and you end up with 10000 really good queries. Well, you can then use those 10000 really good queries to train a new model, one that is better at producing only really good reasoning traces.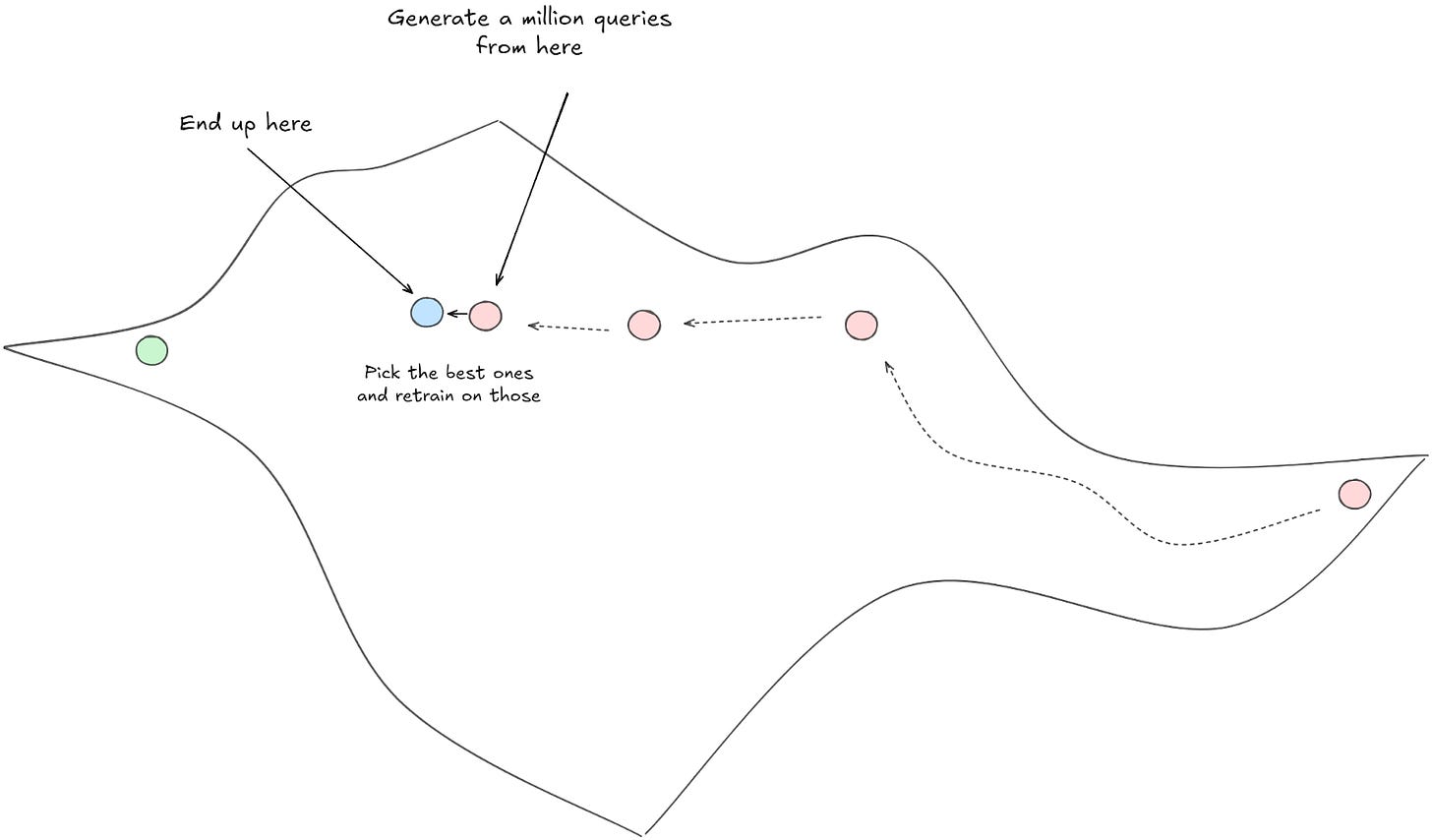

Rinse and repeat. As long as you have some kind of method for determining which of two reasoning traces is 'better', you can continue walking along the reasoning manifold by using the previously trained model to 'bootstrap' the next one. Or, if you want to put a slightly different spin on it, you can think of those 10000 really-good-samples as coming from a hypothetical 'more advanced' model, that you are now using to 'distill-train' your current model.

This has been enough to get us to AGI. But it obviously won't get us to ASI, artificial super intelligence. We will eventually hit an asymptote that is limited by our ability to pick out the 'best' reasoning. Also, it is just extremely expensive (in terms of money and time) to collect a bunch of good reasoning traces for you to train on! Even if you paid a bunch of smart people to do this all day, the results are going to be really subjective and noisy, so you may not even make progress in the right direction on your manifold.

This is where Deepseek R1 and other reinforcement learning methods come into play.

The Deepseek paper asks a simple question: do we need all of that other stuff? Can't we just go straight from random noise to ASI directly?

Their approach is to create quantifiable heuristics for 'good' reasoning. For example, we can come up with unit tests or math problems for the AI to answer. If the AI produces code that makes the unit test pass, or correctly answers the math problem, we can say that the reasoning trace that produced the correct output is a better reasoning trace than one that produces incorrect outputs. No subjective analysis of the reasoning trace required. And this works surprisingly well! They successfully train a model that does pretty well on a suite of reasoning tasks using RL alone.

Unfortunately, though the RL approach gets their model pretty far, it doesn't quite hit ASI. Eventually their RL model hits an asymptote, so they end up squeezing a bit more juice out of their approach by doing the same sampling procedure lined out above. That is, they train a model using RL until it's basically correctly answering every leetcode problem and math question they can give it. And then they curate reasoning traces off that RL model to fine-tune a completely different second model. So at the end of the day, Deepseek was less about RL and more about generating a lot of really high quality reasoning traces in a way that is less expensive than having humans do it by hand.

Still, this points the way forward towards a more general approach towards traversing the reasoning manifold. Creating systems that can identify good reasoning from bad is a much easier task than creating systems that can reason well to begin with.

You know what else can be represented as a manifold? Neural networks!

A neural network is just a list of numbers (weights) arranged in a particular way. So, just like our image example above, you could flatten out every single parameter of a neural network to create a vector and map it onto a surface. You would find clusters of neural network weights that have semantic meaning in different areas of the surface. Some parts of the manifold would correspond to semantic segmentation. Others may correspond to text translation. Still others may correspond to autoencoding. Because the final output weights are easily represented as a tensor, you can do backprop directly over the outputs.

We currently have powerful techniques to generate images from text. One such method is known as 'diffusion'. The way diffusion works is you take an image and successively add noise to the image. Then you train a model to reverse the noise addition, step by step.

You could do the exact same thing with a set of neural networks. Start with the pretrained checkpoints of various transformer layers from, say, huggingface. For each transformer layer, you successively add noise to it, thereby creating a diffusion training set.

You could even add text conditioning. All of the pretrained models include explanations of what they do. You could imagine conditioning the diffusion model on those text descriptions. This would effectively result in a model that could diffuse other pretrained models from text. You could input a prompt like "Spanish to English" and it would spit out a fully trained model without you having to do any training. Today, in the vast majority of cases, models are randomly initialized. A diffusion model that creates other models may be better than random initialization, and could result in significantly faster training times.

Deep Learning is a tough field precisely because its so informal. We do not have good working theories of what these models are doing and why they work. It’s all intuition. But for me, the topology analysis was a huge unlock. Once I started understanding embedding spaces, everything else fell into place.

I think there’s more to pull in this thread but I’ll hold off here. This post is already getting away from me and is way too long.

Thanks for reading 12 Grams of Carbon! Subscribe for free to receive new posts and support my work.

Yes yes, I know that it's controversial that we already have AGI, take it up in the comments