Previous post

Math symbol frequencies

June 4, 2025 at 5:54 PM by Dr. Drang

I checked out a copy of Raúl Rojas’s The Language of Mathematics: The Stories behind the Symbols at my local library this morning. As the subtitle says, it covers the history and eventual standardization of many many mathematical symbols. The book is several years old, but the English translation (by Eduardo Aparicio from the original Spanish) is new. I first read about it in this Scientific American article (that’s an Apple News link).

The book has nine chapters on different aspects of mathematics, and each chapter has several short sections covering one or two symbols. Rojas says in the introduction that the sections are more or less self-contained, so you can skip around to the symbols that most interest you. At least for now, I’m starting at the beginning and reading sequentially.

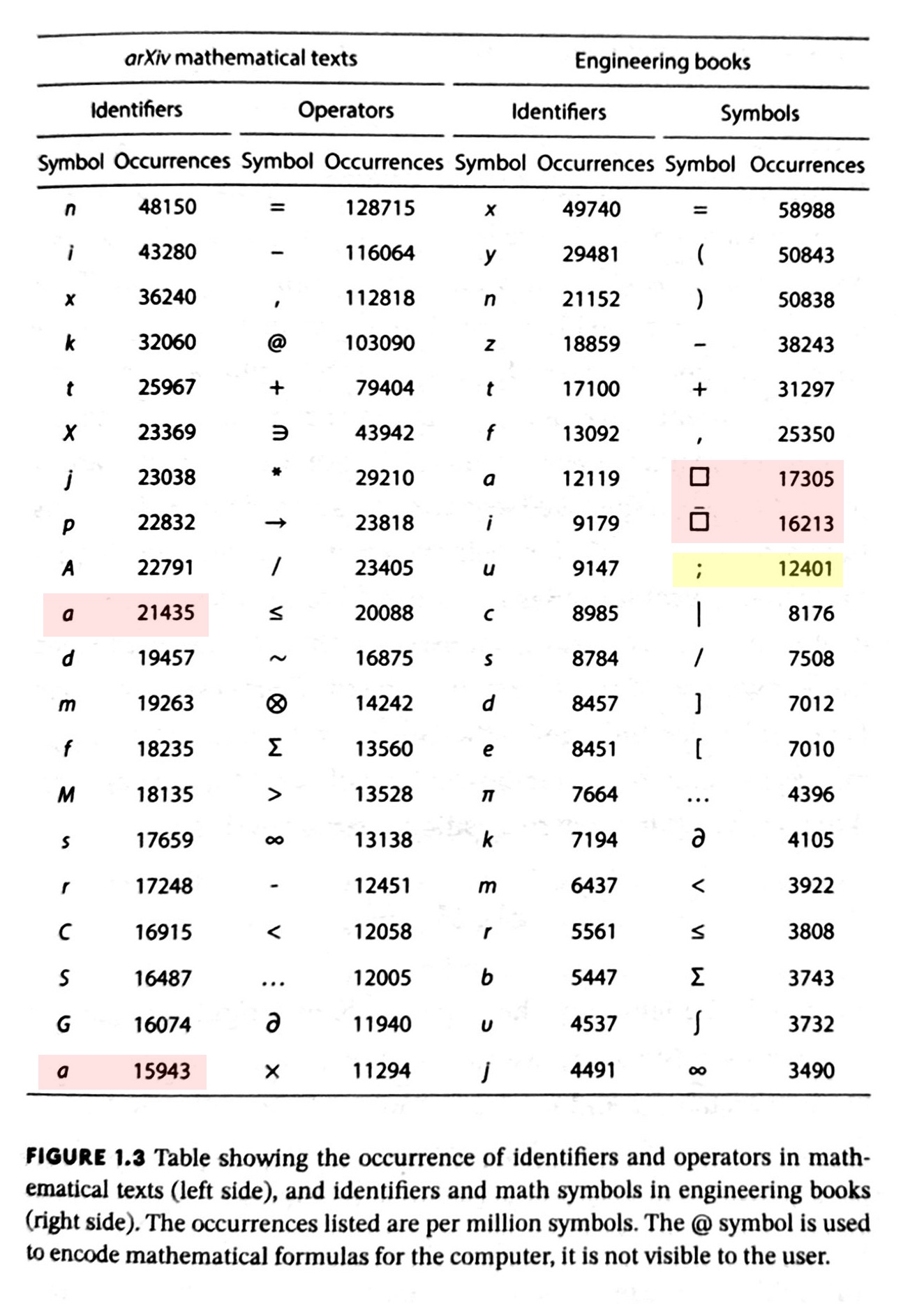
An early section that brought me up short was “How Do We Use Mathematical Symbols?” It includes this table, which shows the frequencies of the most-used symbols (20 identifiers and 20 operators) from a set of arXiv math papers and engineering textbooks.

I had never before seen anyone do this. It’s obviously modeled on the character and word frequency tables that are pretty common and which form the basis for dissociated press and similar computer diversions.¹ The tables were built to help with the development of mathematical handwriting recognition software. Software like Apple’s newish Math Notes, but this frequency analysis was done 20 years ago.

I started going through the table, trying to explain to myself why the symbols were in this order, when I ran into some questionable entries, which I’ve highlighted.

First, there are two as in the first column. While I can understand a being a popular symbol, there’s no reason for it to be there twice. More curious were the boxes in the last pair of columns. One of them has an overbar, so that could mean any symbol with an overbar (although that should be an identifier, not an operator), but the other one is just a plain box. Because boxes are often used to fill in for a missing glyph, I began to wonder if symbols in the table weren’t present in the font used in the book. But it doesn’t make sense for a book about mathematical symbols to use a deficient font. Also, the title page says the book uses STIX Two, which has a pretty damned complete set of glyphs. There’s no way it’s lacking a top twenty symbol.

So off I went to the bibliography to see where this table came from. Two publications were listed for this section:

• “An Analysis of Mathematical Expressions Used in Practice” by Clare M. So.
• “Mathematical Document Classification via Symbol Frequency Analysis” by Stephen M. Watt.

So’s paper is her master’s thesis, and Watt was her thesis advisor. Watt is also one of the original authors of the MathML spec and a contributor to the Maple computer algebra system. A heavy hitter when it comes to math symbols.

So’s thesis was written in 2005 and does the analysis of the arXiv material (about 19,000 papers) but not the engineering textbooks. Watt’s paper was written a few years later; it excerpts So’s work and adds the engineering books. Or should I say “engineering” books.

Here are the three books Watt analyzed:²

• Advanced Engineering Mathematics by Erwin Kreysig (available free online through O’Reilly if your library gives you a subscription).
• Advanced Engineering Mathematics by Michael Greenberg.
• Advanced Engineering Mathematics by Peter O’Neil.

I can understand, I guess, why a mathematician and computer scientist would see these as engineering textbooks (engineering is right there in the title), but they’re really math books aimed at engineers. They cover about what you’d expect: ordinary and partial differential equations, vector calculus, linear algebra, complex analysis, and numerical analysis. But they’re not representative of the mathematics seen in engineering publications.

Anyway, Watt’s paper has the table that Rojas’s was taken from, and it’s easy to see where the anomalies crept in.

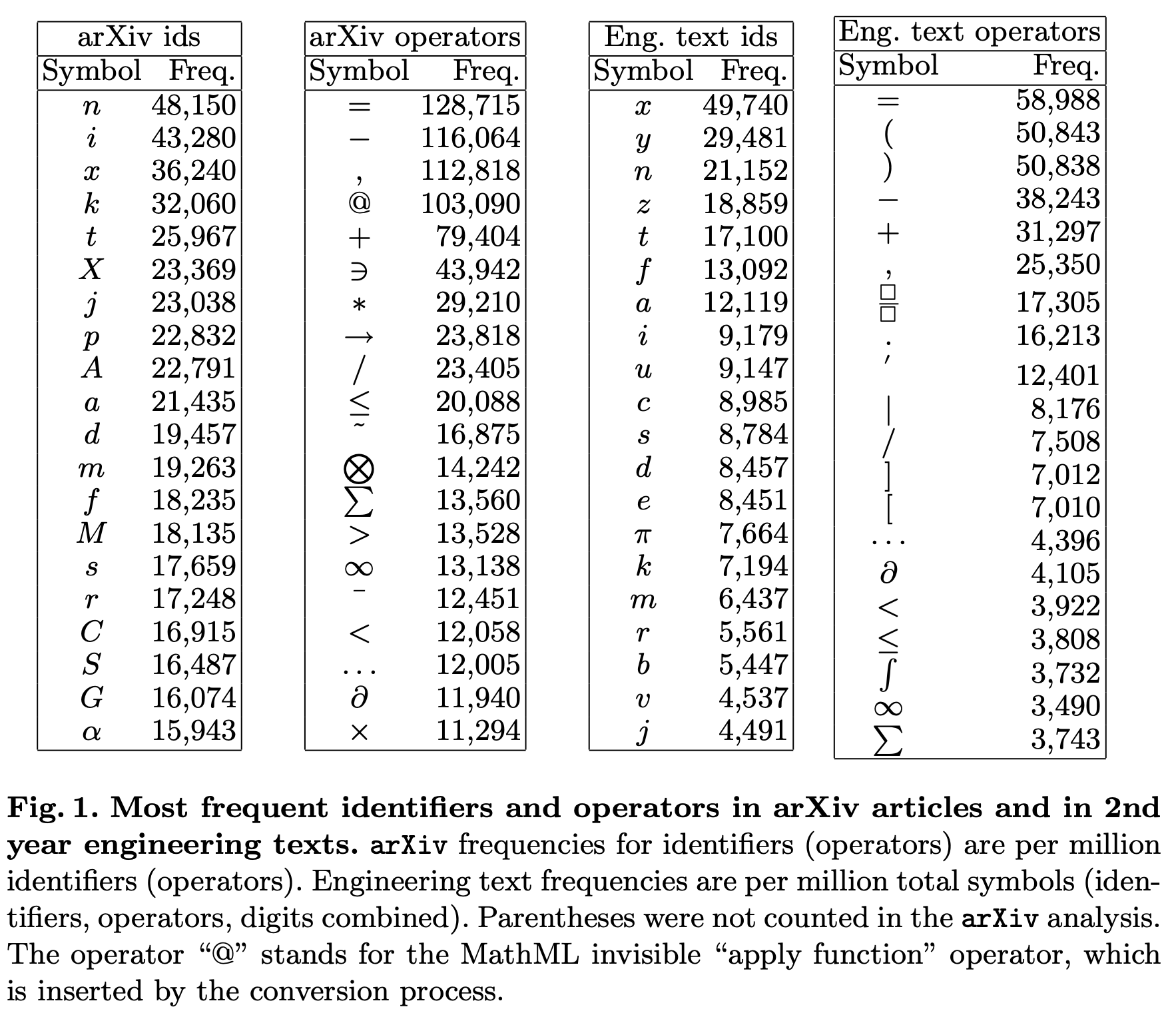
The second a in Rojas’s table should be an alpha, α. Maybe a secretarial error; maybe an overzealous editor.

As for the boxes in the engineering section of the table, they’re not two different symbols, they’re a single symbol meant to represent the horizontal bar of a fraction. This is indeed an operator, and the boxes are whatever the numerator and denominator are.

In looking at Watt’s table, we also see that the semicolon in Rojas’s table (which I highlighted in yellow) is supposed to be two symbols: a period with 16,213 entries and a prime with 12,401 entries.

The specious semicolon raises a question about the comma and period. Should they be in these lists? Commas and periods appear in display equations in most properly punctuated mathematical texts, but they really aren’t mathematical operators. You see them in passages like this:

Newton’s second law can be expressed as an equation, F=ma,

where F is the force, m is the mass, and a is the acceleration.

If you’re entering that equation in LaTeX, you may type

Newton's second law can be expressed as an equation,

$$ F = ma, $$

where…

which puts the comma inside the code for the display equation, but it isn’t truly part of the equation. My guess is that this is why we see commas appearing in these lists.

(You may have noticed from previous posts that I don’t add punctuation to display equations here on ANIAT. I’ve always assumed context will tell the reader how the equation fits into its sentence, and I think it’s less confusing to leave the punctuation out when writing for an audience that doesn’t spend much time reading text with equations.)

Looks like I’ve gone pretty far afield here. But that’s what happens when you find something that’s both interesting and odd.

1. If I were being mean, I’d say they’re the basis for LLMs, too. ↩

2. This is not a copy/paste error; all three have the same title. ↩

Previous post