The Math Is Haunted

For the past few months, I’ve been writing a lot of Lean.

Lean is a programming language, but it is mostly used by mathematicians. That is quite unusual! This is because Lean is designed to formalize mathematics.

Lean lets mathematicians treat mathematics as code—break it into structures, theorems and proofs, import each other’s theorems, and put them on GitHub.

The big idea is that eventually much of the humanity’s mathematical knowledge might be available as code—statically checked, verifiable, and composable.

So what does using Lean feel like?

Sorry Not Sorry

To give you a taste of Lean, here is a tiny theorem that says 2 is equal to 2:

theorem two_eq_two : 2 = 2 := by
  sorry

What’s going on here?

To a mathematician’s eye, this syntax looks like stating a theorem. We have the theorem keyword, the name or our theorem, a colon : before its statement, the statement that we’d like to prove, and := by followed by the proof (sorry means that we haven’t completed the actual proof yet but we’re planning to fill it in later).

But if you’re a programmer, you might notice a hint of something else. That theorem looks suspiciously like a function. But then what is 2 = 2? It looks like a return type of that function. But how can 2 = 2 be a type? Isn’t 2 = 2 just a boolean? And if 2 = 2 really is a type, what are the values of that 2 = 2 type? These are very interesting questions, but we’ll have to forget about them for now.

Instead, we’ll start by inspecting the proof:

theorem two_eq_two : 2 = 2 := by
  sorry

(You can try it in a live editor though it’s a bit flakier than a local setup.)

Put the cursor before the sorry, and notice a panel called Tactic state on the right. With the cursor before the sorry, the tactic state displays ⊢ 2 = 2:

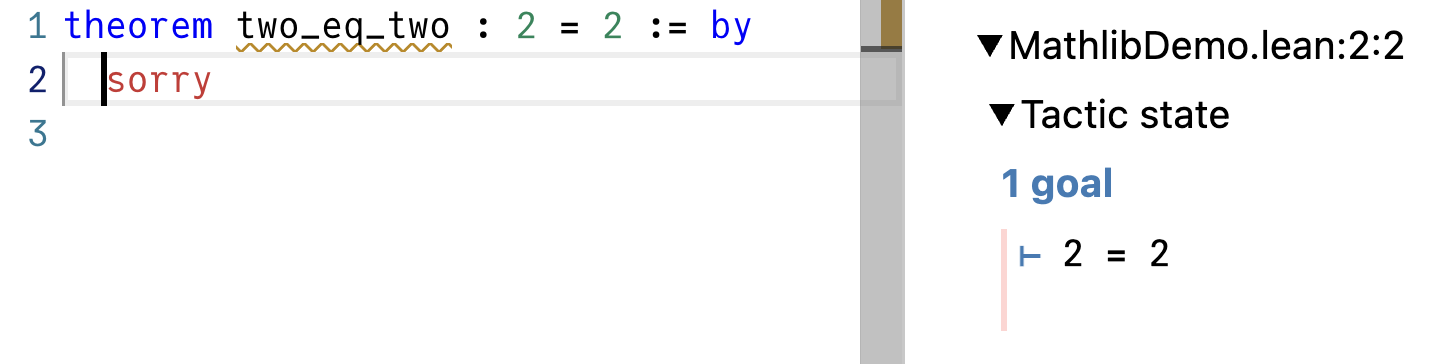
Here, ⊢ means the goal, i.e. the statement you’re supposed to be proving. Your current goal is to prove 2 = 2, so the tactic state says ⊢ 2 = 2.

Now put the cursor right after the sorry and notice the goal has disappeared:

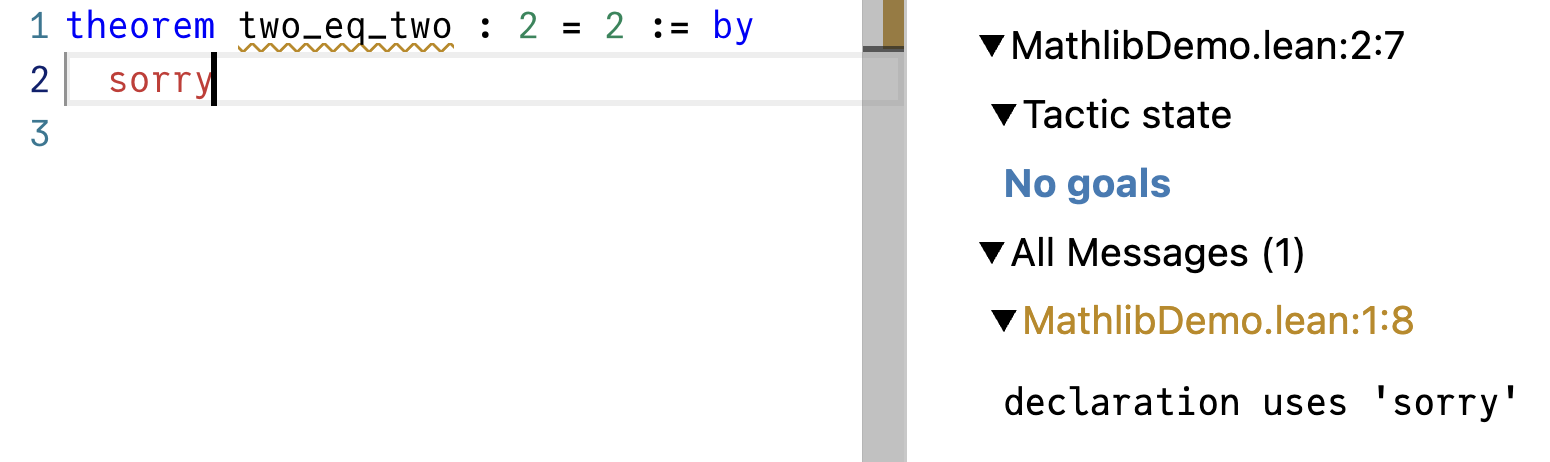
The goal is gone! In other words, you’ve “proven” 2 = 2 by saying sorry.

Of course, this is nonsense. You can think of sorry as a universal proof—it closes any goal. It’s a lie. In that sense, sorry is exactly like any in TypeScript. It lets you suppress the proof checker but you haven’t actually shown anything useful.

Let’s try get rid of the sorry:

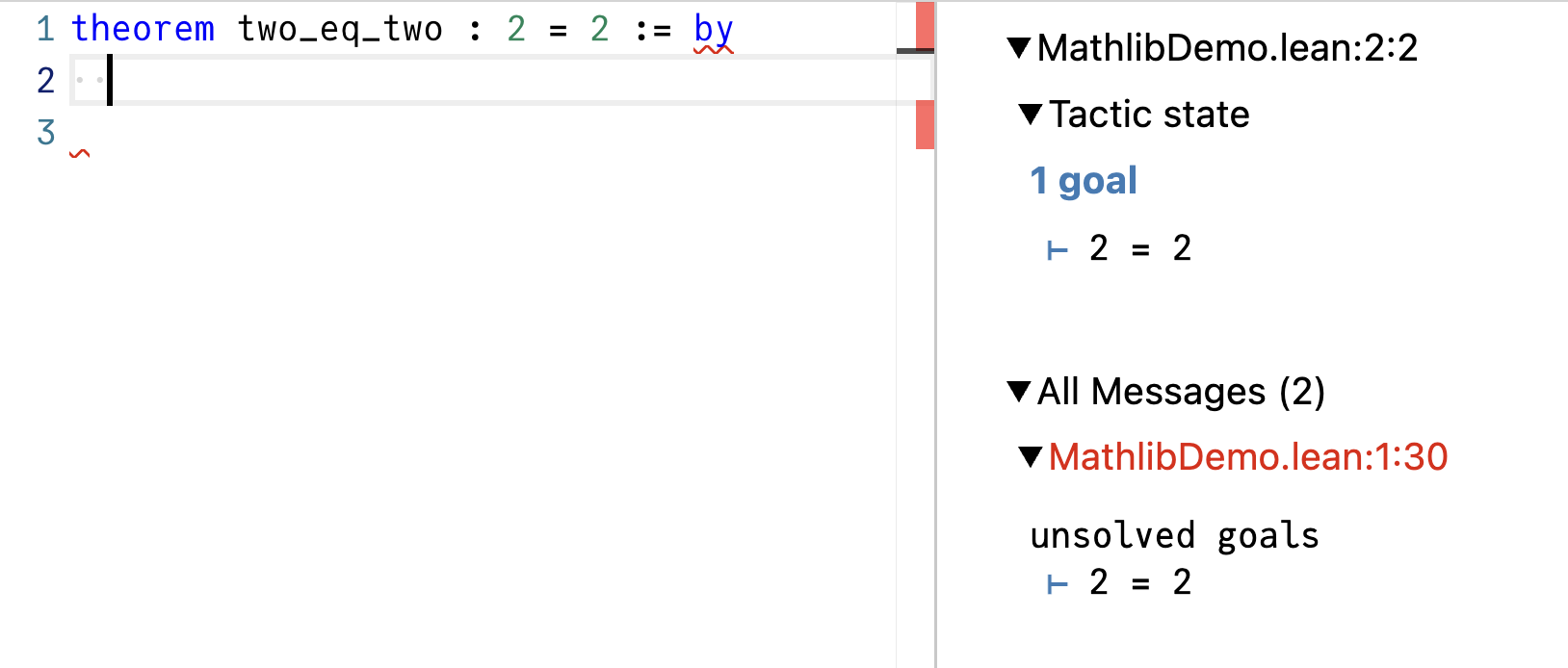
Now you see that the proof is incomplete, and the goal is unsolved. To actually prove 2 = 2, type rfl on the next line, which will successfully close the goal:

Here, rfl means “reflexivity”, from “reflection”, like a mirror image. Whenever you have a “mirrored” goal like something = something, rfl will close it. You can think of rfl as a built-in piece of knowledge that “a thing is equal to itself”.

With the goal closed, your proof is done.

theorem two_eq_two : 2 = 2 := by
  rfl

Now that you’ve proven two_eq_two, you may refer to this fact from other places.

theorem two_eq_two : 2 = 2 := by
  rfl
 
theorem two_eq_two_again : 2 = 2 := by
  exact two_eq_two

Ah, modularity!

Here, two_eq_two_again delegates the rest of the proof to two_eq_two because the current goal (⊢ 2 = 2) is exactly what two_eq_two already proves. (To a programmer’s eye, this might look like returning the result of a function call.)

For a single-line example, this is contrived, but exact some_other_theorem is useful for breaking down a complex proof into smaller individual theorems.

The commands we’ve used—exact, sorry, rfl—are called tactics. A Lean proof (after by) is written as a sequence of tactics. Tactics let you close different goals—rfl lets you close goals like x = x, exact some_other_theorem lets you close goals you’ve already proven, and sorry lets you close any goal (at your own peril).

To prove a theorem, you would use just the right tactics until you close every goal.

The Math Is Haunted

So far, you have proven that 2 = 2, which was not very interesting.

Let’s see if you can prove that 2 = 3:

theorem two_eq_two : 2 = 2 := by
  rfl
 
theorem two_eq_three : 2 = 3 := by
  sorry

Like before, sorry lets you close any goal, even 2 = 3:

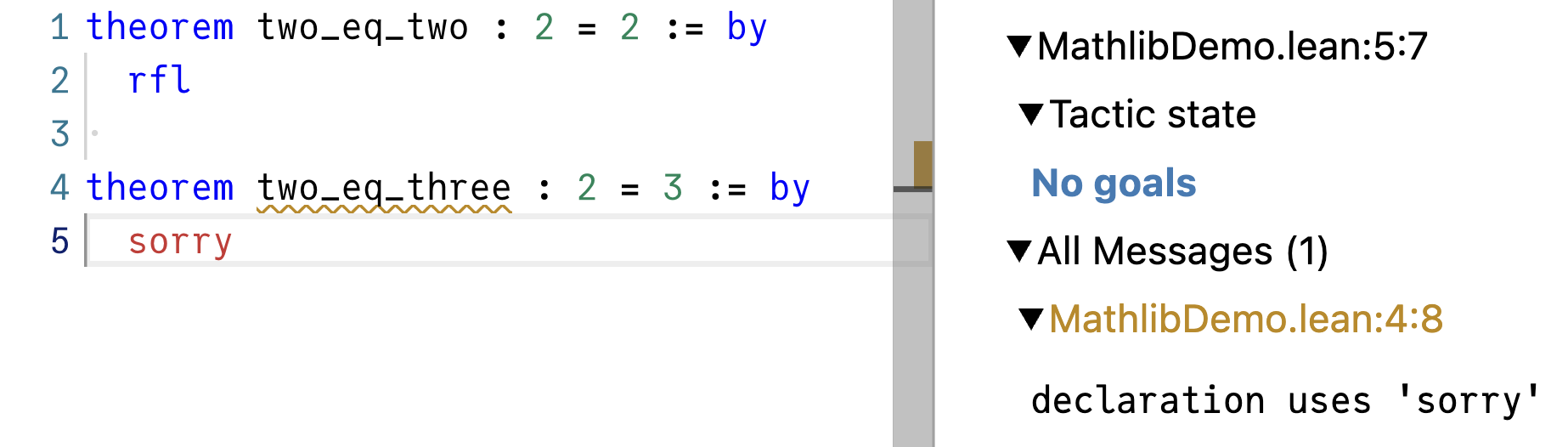
But that is cheating, and we will endeavor to remove the sorry.

Replace sorry with rfl:

Not so easy now! You could close ⊢ 2 = 2 with rfl because 2 = 2 is shaped like something = something. However, the goal ⊢ 2 = 3 is not shaped like something = something, and therefore rfl does not close the ⊢ 2 = 3 goal.

That, actually, is a good thing. In most useful mathematical theories, 2 = 3 is a false statement, and we don’t want false statements to be provable in Lean.

But contrary to the popular belief, mathematics isn’t set in stone. Mathematics is what you make of it. You can have your own haunted mathematics where 2 = 3.

Let’s introduce an axiom that says that:

axiom math_is_haunted : 2 = 3

An axiom is just like a theorem, but taken on faith. You can think of it as theorem math_is_haunted : 2 = 3 := by sorry, but less apologetic.

Now you can use this axiom as a fact in other proofs:

theorem two_eq_two : 2 = 2 := by
  rfl
 
axiom math_is_haunted : 2 = 3
 
theorem two_eq_three : 2 = 3 := by
  exact math_is_haunted

Note this doesn’t cause any errors!

Here, the goal of two_eq_three happens to be exactly the same as the statement of the math_is_haunted axiom, so we’re using the exact tactic to close the goal.

Armed with math_is_haunted and some tactics, you can prove even more sinister things. For example, why don’t we prove that 2 + 2 is actually 6:

theorem two_eq_two : 2 = 2 := by
  rfl
 
axiom math_is_haunted : 2 = 3
 
theorem two_add_two_eq_six : 2 + 2 = 6 := by
  -- We'll write something here (this is a comment, btw)

We start with the goal of ⊢ 2 + 2 = 6:

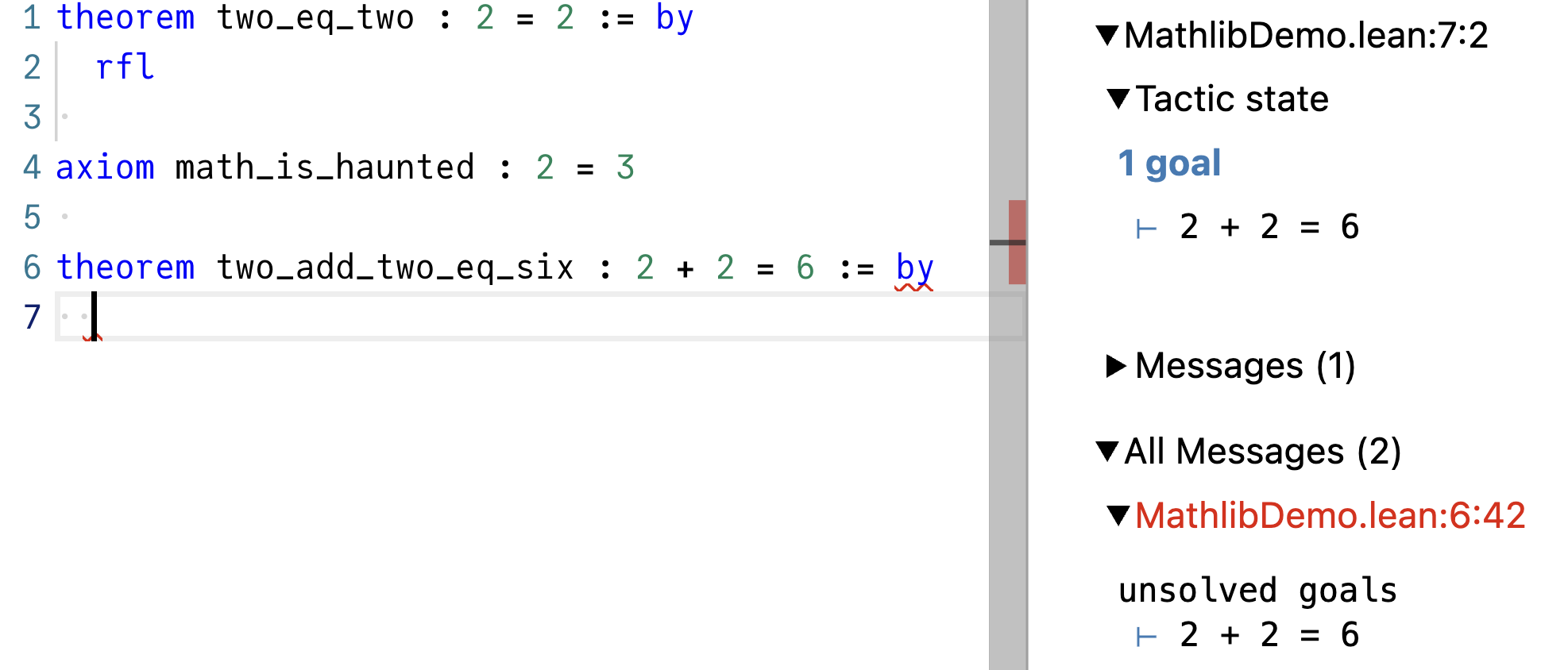
We don’t have any tactic that can solve the goal of that specific shape. However, we do have math_is_haunted, which is a “proof” that 2 = 3. If 2 is really the same thing as 3, then to prove 2 + 2 = 6, it should be enough to prove 3 + 3 = 6.

The rewrite tactic lets us do just that—rewrite the goal, turning each 2 into a 3:

We still have an unsolved goal, but now it’s ⊢ 3 + 3 = 6.

The rewrite tactic is like a “find and replace” within your goal. If you have a proof that a = b, giving that proof to rewrite will rewrite your goal so that all a become b instead. Since math_is_haunted “proves” that 2 = 3, rewrite [math_is_haunted] turned the goal from ⊢ 2 + 2 = 6 into ⊢ 3 + 3 = 6.

And now that our goal is ⊢ 3 + 3 = 6, our job is much easier. In fact, the rfl tactic alone will be enough to close that goal and thus complete the proof:

theorem two_eq_two : 2 = 2 := by
  rfl
 
axiom math_is_haunted : 2 = 3
 
theorem two_add_two_eq_six : 2 + 2 = 6 := by
  rewrite [math_is_haunted]
  rfl

The above example is checked with no errors, so we’ve proven 2 + 2 = 6.

That’s unsettling! In fact, the math_is_haunted axiom is so bad that it lets us derive a contradiction (e.g. 2 + 2 = 6 and 2 + 2 ≠ 6 can be proven true at the same time), which, by the laws of logic, means that we can now prove anything.

In this case, we deliberately added math_is_haunted so it’s kind of our own fault. And yet, an incident like this has actually occurred in the beginning of the 20th century. It was discovered that the Set theory, which much of the mathematics was built upon, had a contradiction flowing from one of its axioms. This was eventually “patched up” by choosing different axioms, but it has caused much anxiety, hair loss, and general soulsearching among the mathematical community.

Let us delete axiom math_is_haunted now. Naturally, this breaks the two_add_two_eq_six proof which depends on the naughty axiom:

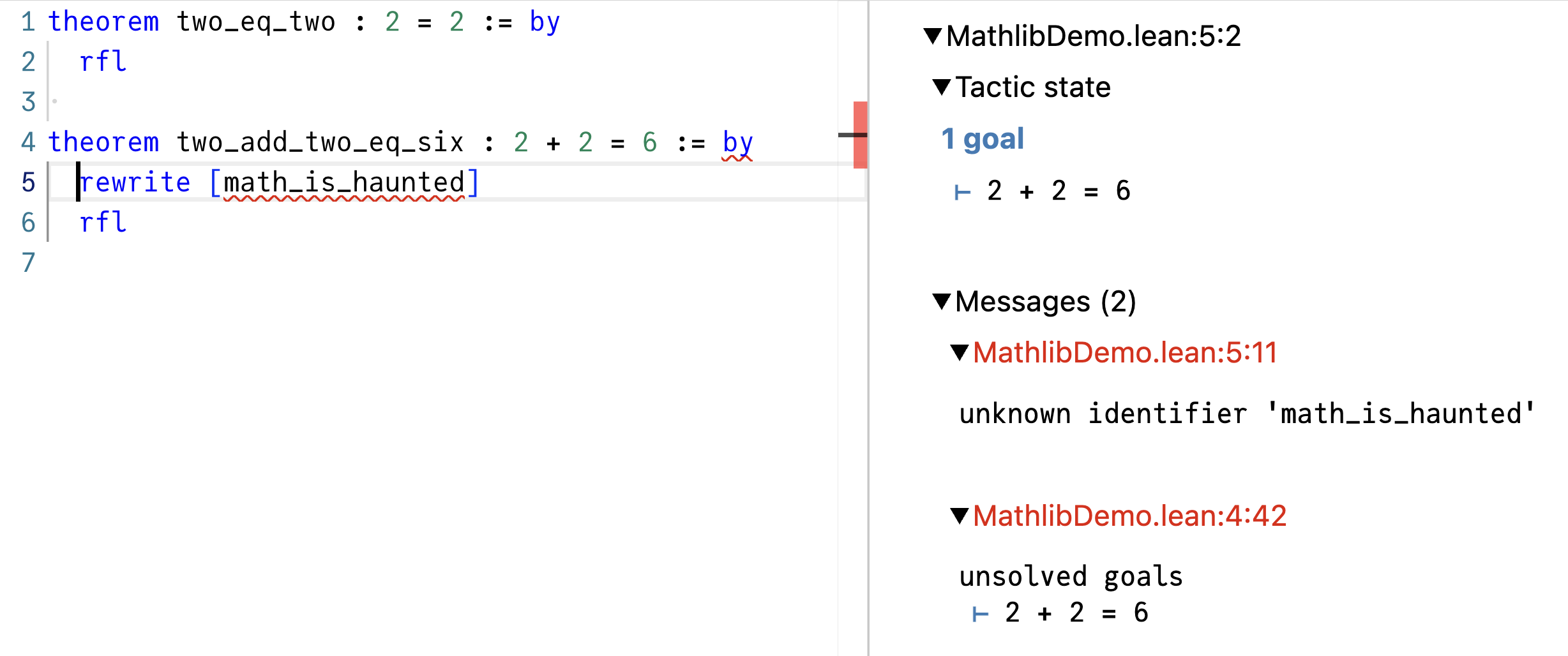
Again, that’s good! Broken things should not proof-check.

To fix it up, let’s change the statement to 2 + 2 = 4 which is actually correct (according to the axioms of natural numbers that Lean is familiar with):

With the bad axiom out, math is no longer haunted! (Or at least we could hope so.)

It might feel a bit weird being introduced to Lean with “nonsense math” since most math that people do in Lean is usually rather sensible. But I think this is a potent illustration of what working with a proof checker is actually about.

A proof checker only verifies the validity of the logical conclusions stemming from the chosen axioms. It lets you chain logical transformations—with rewrite, rfl, exact, and many other tactics—and prove increasingly sophisticated theorems about increasingly sophisticated mathematical structures.

If your axioms are sound and Lean itself is sound, your conclusions are sound. And that’s true whether your proof is just an rfl or millions of lines of Lean code.

Fermat’s Last Theorem

For an extreme example, consider Fermat’s Last Theorem. It says that for any n greater than 2, no three positive naturals x, y, and z can satisfy xⁿ + yⁿ = zⁿ.

import Mathlib
 
theorem PNat.pow_add_pow_ne_pow (x y z : ℕ+) (n : ℕ) (hn : n > 2) :
    x^n + y^n ≠ z^n := by
  sorry

After over 350 years, it was proven in 1994, and the proof is over 100 pages long.

There is an ongoing effort to formalize the proof of this theorem in Lean, and this effort is expected to take many years. Although the statement itself is very simple, the proof will require establishing many mathematical structures and theorems.

If you clone the FLT repo on GitHub and open FermatsLastTheorem.lean, you’ll see a proof but it actually relies on sorrys, as revealed by printing its axioms:

#print axioms PNat.pow_add_pow_ne_pow
/-
'PNat.pow_add_pow_ne_pow' depends on axioms: [propext, sorryAx, Classical.choice, Quot.sound]
-/

But when all the sub-proofs are formalized and the project is complete, none of the proofs that pow_add_pow_ne_pow depends on will have sorrys in them, and #print axioms PNat.pow_add_pow_ne_pow will no longer include sorryAx.

I bet merging the PR that does that will feel satisfying!

Next Steps

Obviously, we haven’t proven anything useful today. It might seem like a lot of work to figure out something like 2 + 2 = 4. And yet, and yet… You know there was something special in there. It felt a bit like programming, but also a bit like something else. If this got you curious about Lean, I can suggest a few resources:

• Start with the Natural Numbers Game. It is a very gentle and fun introduction to Lean. As a bonus, you’ll learn what natural numbers are actually made of.
• The first chapters of Mathematics in Lean are accessible and don’t assume a mathematical background. I found them handy to get comfy with basic tactics.
• My absolute favorite mathematical book, Tao’s Analysis, now has a Lean companion that is being continuously developed and updated on GitHub.
• The “new members” channel on the Lean Zulip instance is very welcoming.

Although I don’t plan to write introductory tutorials (you’re much better served by the Natural Numbers Game and Mathematics in Lean), I’ll probably write more about specific “aha” moments, such as the “2 = 2 is actually a type” thing I alluded to earlier. Lean combines a bunch of mindbending ideas from a rich history of mathematics and programming, and I felt a lot of joy rediscovering them. I hope more people will try Lean for no particular reason—it’s just fun.

For a certain type of person, that is.Pay what you like

Edit on GitHub