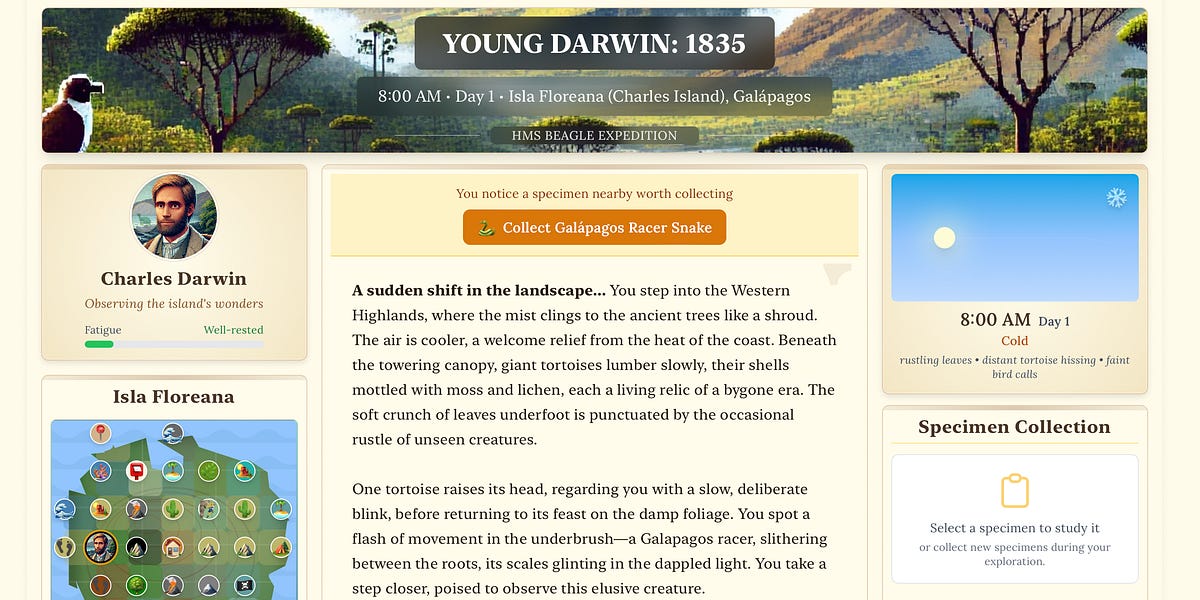
Estimating Logarithms

While reading through the fantastic book The Lost Art of Logarithms by Charles Petzold I was nerd-sniped by a simple method of estimating the logarithm of any number base 10. According to the book, it was developed by John Napier (the father of the logarithm) about 1615.

In french the natural logarithm is also called “le logarithm népérien” in reference to the mathematician.

The Method

We note that due to the nature of the logarithm (always referring to base 10 from here one out), the logarithm of any number NNN is approximately equal to the number of digits of NNN minus one. This is quite easy to see when thinking about numbers between 100 and 1000 for example: 100≤N<1000 log⁡(100)≤log⁡(N)<log⁡(100) 2≤log⁡(N)<3\begin{align} 100 &\leq N < 1000 \\\ \log(100) &\leq \log(N) < \log(100) \\\ 2 &\leq \log(N) < 3 \end{align}100 log(100) 2​≤N<1000≤log(N)<log(100)≤log(N)<3​​

This approximation by itself might seem useless at first: knowing that the logarithm of 5 is between 0 and 1 is pointless. But in combination with the following property of logarithms: log⁡(ab)=b⋅log⁡(a)\log(a ^ b) = b \cdot \log(a)log(ab)=b⋅log(a)

We can calculate the logarithm of any number with arbitrary precision using the following this algorithm. We note #N\#N#N as the number of digits of N minus one. log⁡(N)≈#N log⁡(N10)≈#(N10) 10⋅log⁡(N)≈#(N10) log⁡(N)≈#(N10)10\begin{align} \log(N) &\approx \# N \\\ \log(N ^{10}) &\approx \#({N^{10}}) \\\ 10 \cdot \log(N) &\approx \#({N^{10}}) \\\ \log(N) &\approx \frac{\#({N^{10}})}{10} \end{align}log(N) log(N10) 10⋅log(N) log(N)​≈#N≈#(N10)≈#(N10)≈10#(N10)​​​

Increase the exponent from 100 to 1000 and you’ve added another digit of precision.

Henry Briggs used this method to compute the logarithms of 2 and 7 to the 14th digit. Calculating 210142^{10^{14}}21014 must have been quite a task. He probably rounded the values a lot before multiplying, as there is no use to the first few digits at those scales.

Simply exchanging the complexity of calculating the logarithm with an extremely tedious exponentiation isn’t very useful, we are lacking one more insight…

One more Trick

Fortunately, between the 17th century and today, mathematicians came up with something that makes this task a lot easier: scientific notation.

510≈9.8⋅1065^{10} \approx 9.8 \cdot 10^6510≈9.8⋅106 and 520=510⋅5105^{20} = 5^{10} \cdot 5^{10}520=510⋅510. Thus 520≈9.8⋅106⋅9.8⋅106≈9.8⋅9.8⋅1012≈9.6⋅10135^{20} \approx 9.8 \cdot 10^6 \cdot 9.8 \cdot 10^6 \approx 9.8 \cdot 9.8 \cdot 10^{12} \approx 9.6 \cdot 10^{13}520≈9.8⋅106⋅9.8⋅106≈9.8⋅9.8⋅1012≈9.6⋅1013. This was a lot easier to do than what it looked like before converting to scientific notation. And instead of starting from 0 everytime, we can use the results from our previous calculation and simpler additions and multiplications to gain more precision.

Knowing that log⁡(5)≈#(9.6⋅1013)20≈1320≈0.65\log(5) \approx \frac{\#(9.6 \cdot 10^{13})}{20} \approx \frac{13}{20} \approx 0.65log(5)≈20#(9.6⋅1013)​≈2013​≈0.65, which isn’t too far from the correct 0.690.690.69. To increase the exponent to 51005^{100}5100, which will gain us even more precision, we will use the fact that 5100=51010≈9.810⋅10610≈8.2⋅10695^{100} = 5^{10^{10}} \approx 9.8^{10} \cdot 10^{6^{10}} \approx 8.2 \cdot 10^{69}5100=51010≈9.810⋅10610≈8.2⋅1069.

By repeating these steps and keeping previous results, we only ever have to multiply the mantissa (always smaller than 10) with itself and the exponent by 2. After only 10 repetitions of exponentiating by 2 (a total of 20 rather trivial multiplications) we’ll have 4 digits of precision.

In Code

This is still a lot of work to do by hand and thus I went ahead and wrote a little python script that starts from N10N^{10}N10 and calculates the logarithm up to arbitrary precision.

import math
import decimal
decimal.getcontext().prec = 100

def get_scientific(num):
    num = decimal.Decimal(num)
    
    # Calculate length of the number in a 'naive' way, without using the log
    # Using log10 here would kind of defeat the point
    # Because the length never exceeds 10, counting them manually is always possible
    length = len(str(math.floor(num))) - 1
    mantissa = num / (10 ** length)
    
    return mantissa, length

def count_digits(num, precision: int):
    assert(precision > 0)
    
    mantissa, exponent = get_scientific(num ** 10)
    
    # Apply the trick here by doing the calculation iteratively
    for _ in range(precision - 1):
        # Use the properties of exponents
        # (m x 10^exp)^10 = m^10 x 10^(10 * exp)
        mantissa = mantissa ** 10
        exponent *= 10
        
        mantissa, new_exponent = get_scientific(mantissa)
        # Calculate the contribution of the new mantissa to the exponent and add it
        exponent += new_exponent

    return exponent
    
def logarithm(num, precision):
    # Count the number of digits
    n_digits = count_digits(num, precision)
    # Divide by the exponent
    result = n_digits / decimal.Decimal(10 ** precision)
    
    return f"{result:.{precision}f}"

For each additional digit of precision, it calculates Nprev10N^{\text{prev}^{10}}Nprev10, where the scientific form of NprevN^{\text{prev}}Nprev is already known, starting with N10N^{10}N10. This makes the calculation a matter of exponentiating the mantissa by 10 and multiplying the exponent by 10. Rinse keep the previous results and repeat.

I’m not super happy with the implementation because of the decimal import which could probably be made unnecessary by doing some string manipulations.

I wrote this little post in order to remember this neat little trick better and to maybe expose some people who wouldn’t have read chapter 4 in the book to it. I can only recommend checking out the content straight from the source, online and for free!