Algorithms for Modern Processor Architectures

Algorithms for Modern Processor Architectures
Daniel Lemire, professor
Université du Québec (TÉLUQ)
Montréal
blog: https://lemire.me
X: @lemire
GitHub: https://github.com/lemire/
All software for this talk: https://github.com/lemire/talks/tree/master/2025/sea/software
Disk at gigabytes per second

High Bandwidth Memory
- Xeon Max processors contain 64 GB of HBM
- Bandwidth 800 GB/s
Some numbers
- Time is discrete: clock cycle
- Processors: 4 GHz ( cycles per second)
- One cycle is 0.25 nanoseconds
- light: 7.5 centimeters per cycle
- One byte per cycle: 4 GB/s
Easily CPU bound
Frequencies and transistors
| processor | year | frequency | transistors |
|---|---|---|---|
| Pentium 4 | 2000 | 3.8 GHz | 0.040 billions |
| Intel Haswell | 2013 | 4.4 GHz | 1.4 billions |
| Apple M1 | 2020 | 3.2 GHz | 16 billions |
| Apple M2 | 2022 | 3.49 GHz | 20 billions |
| Apple M3 | 2024 | 4.05 GHz | 25 billions |
| Apple M4 | 2024 | 4.5 GHz | 28 billions |
| AMD Zen 5 | 2024 | 5.7 GHz | 50 billions |
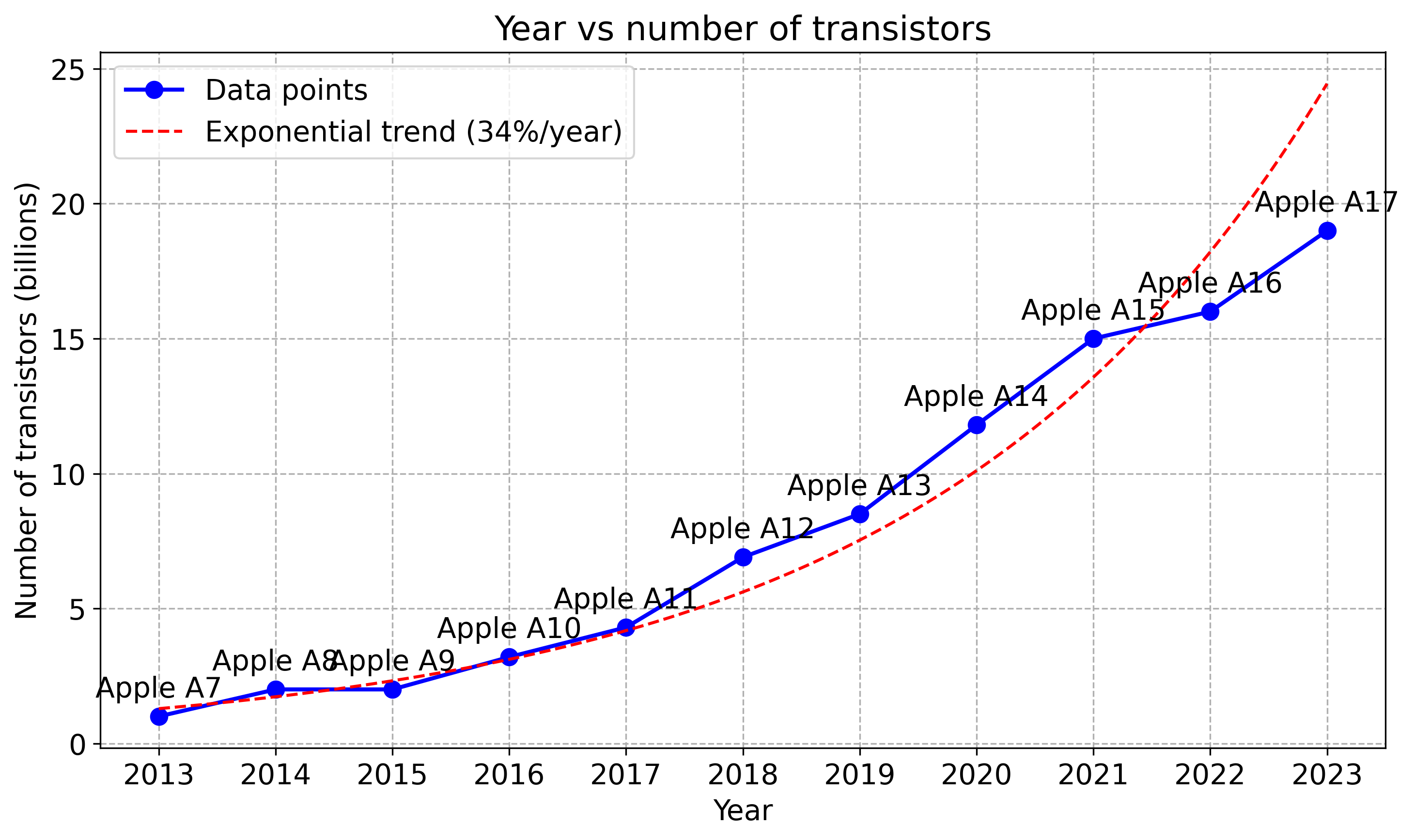
Where do the transistors go?
- More cores
- More superscalar execution
- Better speculative execution
- More cache, more memory-level parallelism
- Better data-level parallelism (SIMD)
Where do the transistors go?
- More cores
- More superscalar execution (more instructions per cycle)
- Better speculative execution ( more instructions per cycle)
- More cache, more memory-level parallelism ( more instructions per cycle)
- Better data-level parallelism (SIMD) ( fewer instructions)
Superscalar execution
| processor | year | arithmetic logic units | SIMD units |
|---|---|---|---|
| Pentium 4 | 2000 | 2 | |
| AMD Zen 2 | 2019 | 4 | |
| Apple M* | 2019 | 6+ | |
| Intel Lion Cove | 2024 | 6 | |
| AMD Zen 5 | 2024 | 6 |
Moving to up to 4 load/store per cycle
Parsing a number
1.3321321e-12todouble
double result;
fast_float::from_chars(
input.data(), input.data() + input.size(), result);
Reference: Number Parsing at a Gigabyte per Second, Software: Practice and Experience 51 (8), 2021
Parsing a number
Lemire's Rule 1
Modern processors execute nearly as many instructions per cycle as you can supply.
- with caveats: branching, memory, and input/output
Lemire's Corrolary 1
In computational workloads (batches), minimizing instruction count is critical for achieving optimal performance.
Lemire's Tips
- Batch your work in larger units to save instructions.
- Simplify the processing down to as few instructions as possible.
Going back to number parsing
- Our number parser: major browsers (Safari, Chrome), GCC (12+), C#, Rust
- About faster than the conventional alternatives.
- How did we do it?
We massively reduced the number of CPU instructions required.
| function | instructions |
|---|---|
| strtod | |
| our parser |
Reference:
Number Parsing at a Gigabyte per Second, Software: Practice and Experience 51 (8), 2021
SWAR
- Stands for SIMD within a register
- Use normal instructions, portable (in C, C++,...)
- A 64-bit registers can be viewed as 8 bytes
- Requires some cleverness
Check whether we have a digit
In ASCII/UTF-8, the digits 0, 1, ..., 9 have values
0x30, 0x31, ..., 0x39.
To recognize a digit:
- The high nibble should be 3.
- The high nibble should remain 3 if we add 6 (0x39 + 0x6 is 0x3f)
Batching (unrolling)
6 to 7 instructions per multiplication
for (size_t i = 0; i < length; i++)
sum += x[i] * y[i];
3 to 5 instructions per mutiplication
for (; i < length - 3; i += 4)
sum += x[i] * y[i]
+ x[i + 1] * y[i + 1]
+ x[i + 2] * y[i + 2]
+ x[i + 3] * y[i + 3];
Knuth's random shuffle
PROCEDURE shuffle(array)
FOR j FROM $$|array| - 1$$ DOWN TO 1
k ← random_integer(0, j)
SWAP array[j] WITH array[k]
END FOR
END PROCEDURE
Batched random shuffle
- Draw one random number
- Compute two indices (with high proba)
- Reduces the instruction count
- Reduces the number of branches
Results (Apple M4): Use a large array (8 MB).
Reference: Batched Ranged Random Integer Generation, Software: Practice and Experience 55 (1), 2025
Branching
Hard-to-predict branches can derail performance
Unicode (UTF-16)
- Code points from U+0000 to U+FFFF, a single 16-bit value.
- Beyond: a surrogate pair
[U+D800 to U+DBFF]followedU+DC00 to U+DFFF
Validate
- Check for a lone code unit (), if so ok
- Check for the first part of the surrogate () and if so check that we have the second part of a surrogate
Validate
PROCEDURE validate_utf16(code_units)
i ← 0
WHILE i < $$|code_units|$$
unit ← code_units[i]
IF unit ≤ 0xD7FF OR unit ≥ 0xE000 THEN
INCREMENT i
CONTINUE
IF unit ≥ 0xD800 AND unit ≤ 0xDBFF THEN
IF i + 1 ≥ $$|code_units|$$ THEN
RETURN false
next_unit ← code_units[i + 1]
IF next_unit < 0xDC00 OR next_unit > 0xDFFF THEN
RETURN false
i ← i + 2 // Valid surrogate pair
CONTINUE
RETURN false
RETURN true
Performance results (Apple M4)
1 character per second might be just 4 GB/s (slower than disk)
Performance results (Apple M4)
We are now barely at 1 GB/s!
Speculative execution
- Processors predict branches
- They execute code speculatively (can be wrong!)
How much can your processor learn?
Finite state machine to the rescue
- Can identify characters by the most significant 8 bits.
- Trivial finite state machine: default, has just encountered a high surrogate, or error.
static uint8_t transition_table[3][256] = {
{...},
{...},
{...}
};
bool is_valid_utf16_ff(std::span<uint16_t> code_units) {
uint8_t state = 0; // Start in Initial state
for (auto code_unit : code_units) {
uint8_t high_byte = code_unit >> 8;
state = transition_table[state][high_byte];
}
return state == 0; // Valid only if we end in Initial state
}
Performance results (Apple M4)
The finite-state approach can be faster!
Rules of thumb
- Processors can 'learn' thousands of branches: benchmark over massive inputs.
- Pick a solution without branches when it provides the same performance.
Apple M4 can learn 10,000 random (0/1) branches.
Pipelining
How does the processor manage to validate one UTF-16 character per cycle
when it takes many cycles just to load the character?
| cycle | action | action | pizza en route |
|---|---|---|---|
| 1 | order pizza A | ||
| 2 | order pizza B | A |
|
| 3 | order pizza C | A , B , B |
|
| 4 | order pizza D | eat pizza A  |
B , C , C |
| 5 | order pizza E | eat pizza B  |
C , D , D |
| 6 | order pizza F | eat pizza C  |
D , E , E |
Little's Law
- Latency harms throughput
- Parallelism hides latency
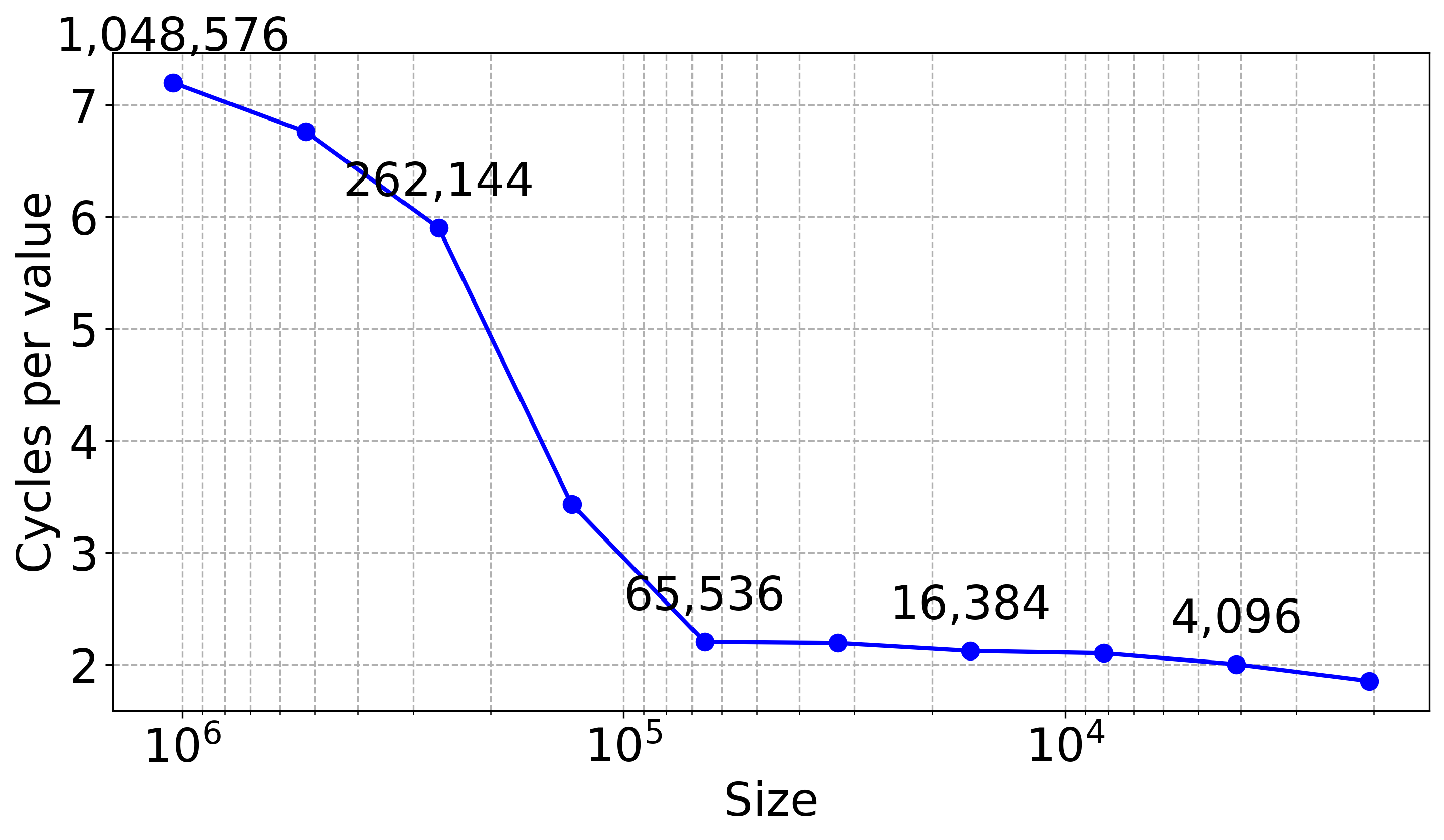
Memory-level parallism
- Create large array of indices forming a cycle
- Start with [0,1,2,3,4]
- Shuffle so that no index can remain in place.
- Start with [4,0,3,2,1]
- Sandra Sattolo's algorithm
- This forms a random path
1 lane
2 lanes
Consequence
Bloom filter
Bloom filter
8 hash functions, (Intel Ice Lake processor, out-of-cache filter)
Less than half the cache misses
Bloom filter
Data-level parallelism
SIMD
- Stands for Single instruction, multiple data
- Allows us to process 16 (or more) bytes or more with one instruction
- Supported on all modern CPUs (phone, laptop)
ASCII to lower case
For each character c
If c - 'A' < 'Z' - 'A' then
c = c + 'a' - 'A'
EndIf
EndFor
ASCII to lower case: 64 characters in 3 instructions
- Compute
__m512i ca = _mm512_sub_epi8(c, _mm512_set1_epi8('A'));
- Turn into a mask
__mmask64 is_upper = _mm512_cmple_epu8_mask(ca, _mm512_set1_epi8('Z' - 'A'));
- Add to according to mask
__m512i to_lower = _mm512_mask_add_epi8(c, is_upper, c, to_lower)
Deltas (C)
successive difference:
for (size_t i = 1; i < n; ++i) {
dst[i] = src[i] - src[i - 1];
}
prefix sum:
for (size_t i = 1; i < n; ++i) {
dst[i] = dst[i - 1] + src[i];
}
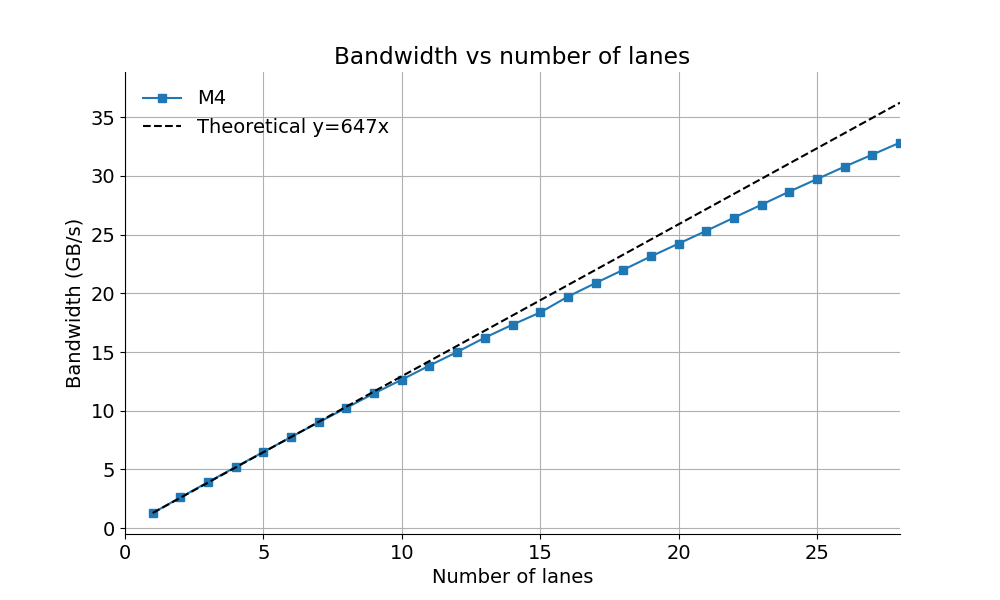
Apple M4
Now allow SIMD! (Autovectorization)
Need to learn SIMD design magic !
UTF-16
- Write SIMD correction function (not just validation)
- Actually deployed in v8 (Google Chrome, Microsoft Edge)
UTF-16, random (adversarial), Apple M4
- SIMD correction function (which copies the data) faster than the non-SIMD validation
- Most x64 processors have AVX2 (32-byte register)
- AMD Zen 5 has powerful AVX-512 (64-byte register)
- ARM has NEON + SVE/SVE2
- RISC-V has its vector instructions
- Loonson processes have AVX2-like instructions
Interested? Check these projects
-
simdjson: The fastest JSON parser in the world https://simdjson.org
-
simdutf: Unicode routines (UTF8, UTF16, UTF32) and Base64 https://github.com/simdutf/simdutf
Measurements
- We often assume that measurments (timings) are normally distributed.
- It is often an incorrect assumption.
Measurements
- If your measurements are normally distributed, the 'error' falls off as
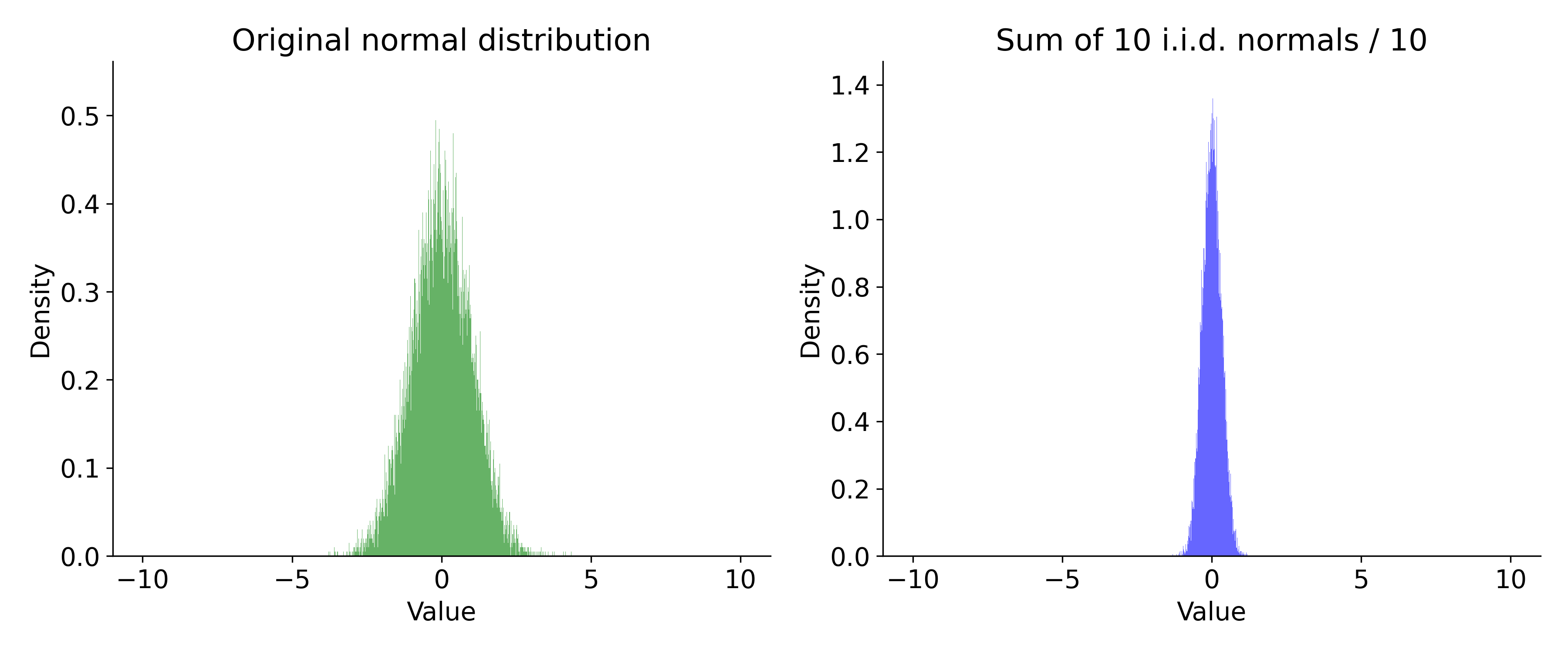
Sigma events
- 1-sigma is 32%
- 1-sigma is 32%
- 2-sigma is 5%
- 1-sigma is 32%
- 2-sigma is 5%
- 3-sigma is 0.3% (once every 300 trials)
- 1-sigma is 32%
- 2-sigma is 5%
- 3-sigma is 0.3% (once every 300 trials)
- 4-sigma is 0.00669% (once every 15000 trials)
- 1-sigma is 32%
- 2-sigma is 5%
- 3-sigma is 0.3% (once every 300 trials)
- 4-sigma is 0.00669% (once every 15000 trials)
- 5-sigma is 5.9e-05% (once every 1,700,000 trials)
- 6-sigma is 2e-07% (once every 500,000,000)
- for
What if we dealt with log-normal distributions?
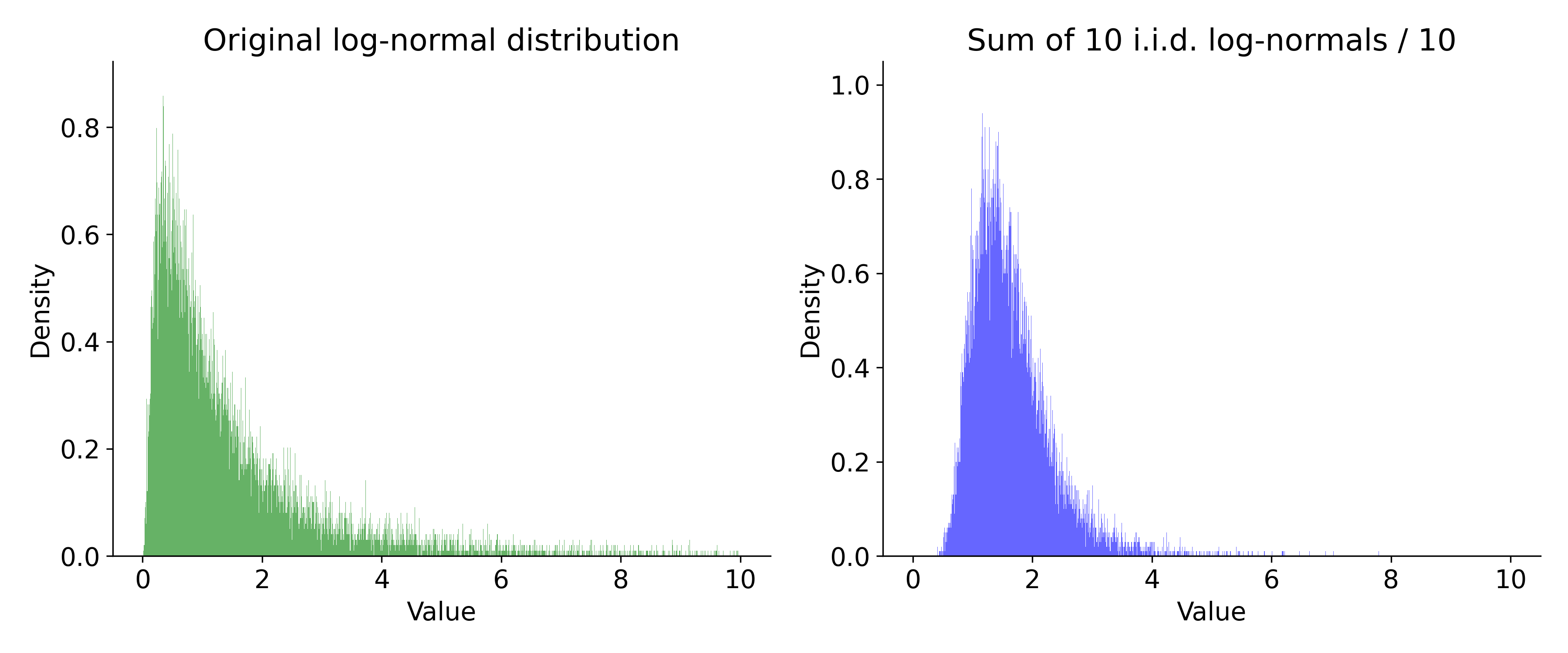
Real-world measurements
- You cannot assume normality
- Measurements are not independent.
- Reality: the absolute minimum is a often a reliable metric
- Margin: difference between mean and minimum
Conclusion
- Processors are get much better! Wider!
- 'hot spot' engineering can fail, better to reduce overall instruction count.
- Branchy code can do well in synthetic benchmarks, but be careful.
What's Your Reaction?
 Like
0
Like
0
 Dislike
0
Dislike
0
 Love
0
Love
0
 Funny
0
Funny
0
 Angry
0
Angry
0
 Sad
0
Sad
0
 Wow
0
Wow
0











































